<問題3>つるかめ算
つるかめ算は、算数の文章題(ぶんしょうだい)の代表的(だいひょうてき)な問題です。

ツルとカメがいる。頭の総数(そうすう)と足の総数がわかるとき、ツルとカメのそれぞれの数はいくらか?
という、問題です。解(と)き方は、次の図をヒントにして自分で考えてみてください。
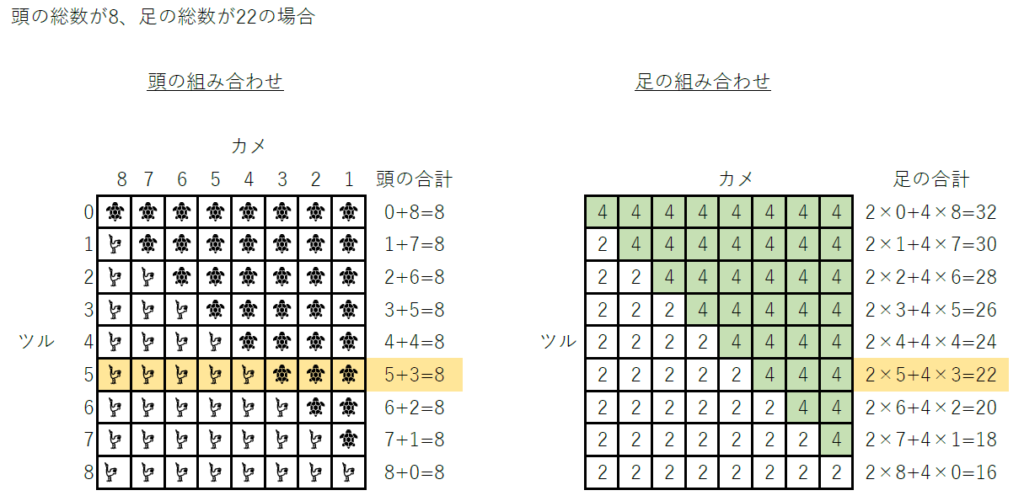
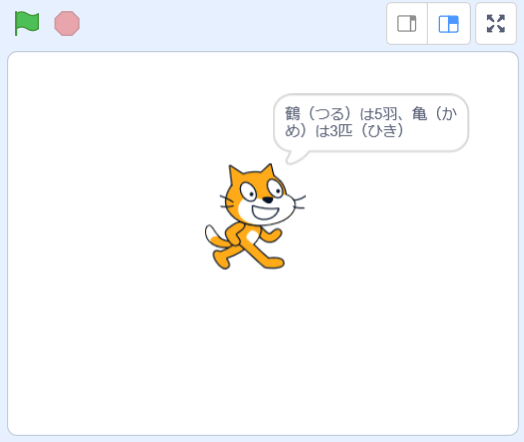
たとえば、頭の総数が8、足の総数が22ときは、ツルが5羽(わ)、カメが3匹(びき)となります。
<数学での解き方>(詳細は省略します)
2元連立一次方程式を解くことにより求まります。
<プログラミングによる解き方>
今回も前回までと同じように、しらみつぶしの方法で解いていきます。上の図をもとに人間が計算するのと同じようにすればよいのです。
※このプログラミング教室でこだわってきた「人間と同じように」というのは、手作業で問題の手順を明らかにしていくことです。このような学習方法を「アンプラグド」あるいは「アンプラグド・プログラミング」といいます。代表的なものが、「CSアンプラグド」(本家:英語、翻訳(ほんやく)サイト:日本語)です。
この例(れい)の場合(ばあい)は、次のように調(しら)べていきます。
| 左の図のように、はじめに、頭の数の8は、すべてカメだと考えます。そうすると、右の図のように「2×0+4×8=32」で、足の合計は32になります。今回は、足の総数が22なのでこれと一致(いっち)しません。 次に、カメを1匹(いっぴき)減らしてツルを1羽増やすと、右の図のように「2×1+4×7=30」で 足の合計は30になります。今回も一致(いっち)しません。 さらに、 カメを減らして6匹(ろくひき)にして、ツルを増やして2羽にして、…、というように続けていきます。 ツルが5羽で、カメが3匹になったとき、右の図のように「2×5+4×3=22」で足の数が条件の「足の総数が22」と一致(いっち)します。 したがって、 ツルが5羽で、カメが3匹ということになります。 答えがもとまったので、これ以上(いじょう)処理を続ける必要(ひつよう)がないのでプログラムは終わりです。 |
以上の処理の流れをまとめると、次のようになります。
- 頭の数をたずねて変数に入れます。
- 足の数をたずねて変数に入れます。
- ツルの数を0にします。
- カメの数を頭の数にします。
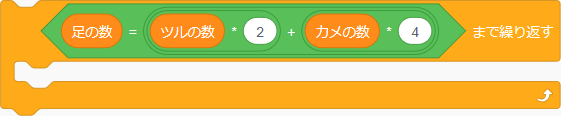
- 「足=ツルの数×2+カメの数×4」という関係が成り立つまで次の処理を繰(く)り返(かえ)します。
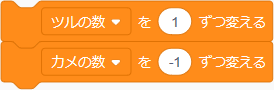
- カメの数を1匹減らします。
- ツルの数を1羽増やします。
- 5の式が成り立ったら繰り返しを終わります。
- 答えを表示して、プログラムを終了します。
<Scratchでプログラミング>
それでは、上でまとめた処理の流れをもとにして、Scratchでプログラムを作ってみましょう。
はじめに、[旗(はた)が押されたとき]ブロックを配置(はいち)します。

処理の中で変化している数は、「 頭の数 」、 「 足の数 」、「ツルの数」、「カメの数」 ですので、この4つを変数として準備します。
変数のコードにおいて[変数を作る]のボタンを押(お)して、次のように新しい変数を作ります。 「 足の数 」、「ツルの数」、「カメの数」 も同じように作ります。
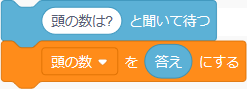
頭の数をたずねて変数に入れるには、つぎのブロックを配置します。
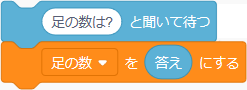
同じように、 足の数をたずねて変数に入れるには、つぎのブロックを配置します。
ツルの数を0にするには、つぎのブロックを配置します。

カメの数を「頭の数」にするには、つぎのブロックを配置します。

続いて、繰返し処理のブロックを配置します。
ツルの数を1羽増やしカメの数を1匹減らすために、次のブロックを上の繰り返し処理のブロックの中に埋(う)め込(こ)みます。
そうすると、つぎのようになります。

最後(さいご)に、 答えを表示 するブロックを追加(ついか)します。

完成(かんせい)した形(かたち)は次のようになります。
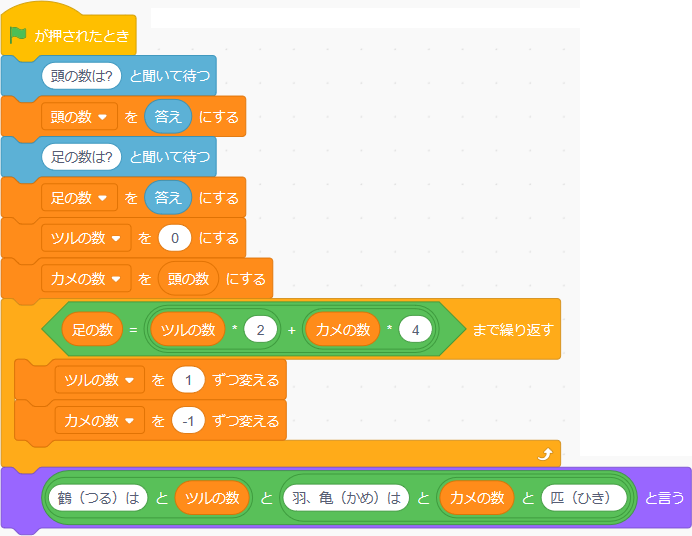
このプログラムを実行すると、キャットが次のように聞いてくるのでそれに答えます。


頭の数と足の数を入力すると、キャットが次のように答えてくれます。
<練習問題3>壷(つぼ)から小判(こばん):オリジナル作問(さくもん)
家の裏庭(うらにわ)を掘(ほ)っていたら、古いつぼが出てきました。中を見ると古銭(こせん)が入っていました。小判(こばん)と銀貨(ぎんか)(1分銀)です。数えてみると、合わせて40枚ありました。また、小判と銀貨の合計の重さをはかると368グラムでした。小判1枚の重さが18グラム、銀貨1枚の重さが7グラムと分かっているとき、小判と銀貨のそれぞれの枚数を求めるプログラムを作成してください。
また、 小判1枚が現在の価値(かち)で5万円、銀貨1枚が1万円とするとき、全部でいくらの価値(金額)になるかも求めてください。
【ヒント】
・上の例とほぼ同じですね。
Copyright (C) 2022 Easy Programming