(1) ピザのサイズ
〔概要〕ピザのサイズを調べるプログラムです。
ある大手ピザチェーンのピザを例にしてピザのサイズを調べます。
次の表のデータのうち黄色の背景で示されている部分が公開されている情報です。そこで、「1.5人前」と明記されているサイズ「P」を基本として計算することにします。ただし、Mサイズの直径が25.4cmとなっていることから10インチがサイズの元になっていると考えられます。なお、この大手ピザチェーンにはSサイズは設定されていないようですが、この例では参考として追加しています。結果を見ると、面積比ではMサイズが1.9人前、Lサイズが3.1人前と想定できます。
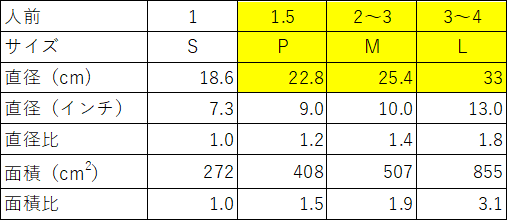
ただし、Sサイズの直径(cm)の「18.6」は、2×√(22.8 / 2) 2/ 1.5で計算するものとします。
〔技法〕リストのリスト(2次元配列)、mathモジュール(円周率、べき乗、平方根)
〔実行例〕
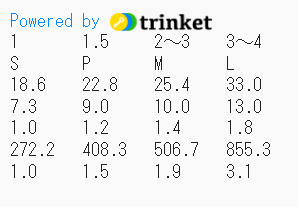
〔プログラム〕
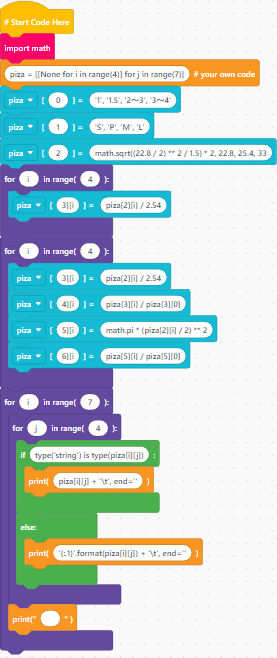
プロジェクトファイル(プログラムファイル):右クリックでダウンロードして、EduBlocksで読み込むことにより実行できます。
(2) 星型多角形(機能限定版)
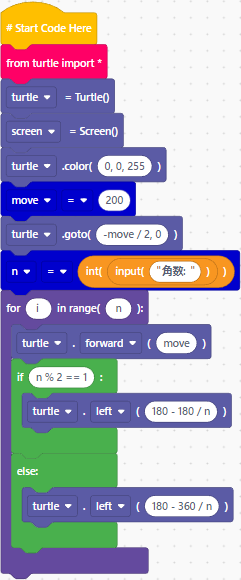
〔概要〕 星型多角形(機能限定版):五芒星を描画するプログラムです。
3角関数を使わず、Turtleグラフィックスの回転と直進だけで描画します。そのため、複合星型正多角形は描画できません。
〔参考文献〕〔m, n〕型の星型多角形の内角の和について、Star Polygon、星型多角形 – Wikipedia、N芒星の数学的側面、星形の角の和の求め方、実践事例2「星型多角形は特殊な図形か」、
〔技法〕Turtleグラフィックス
〔実行例〕
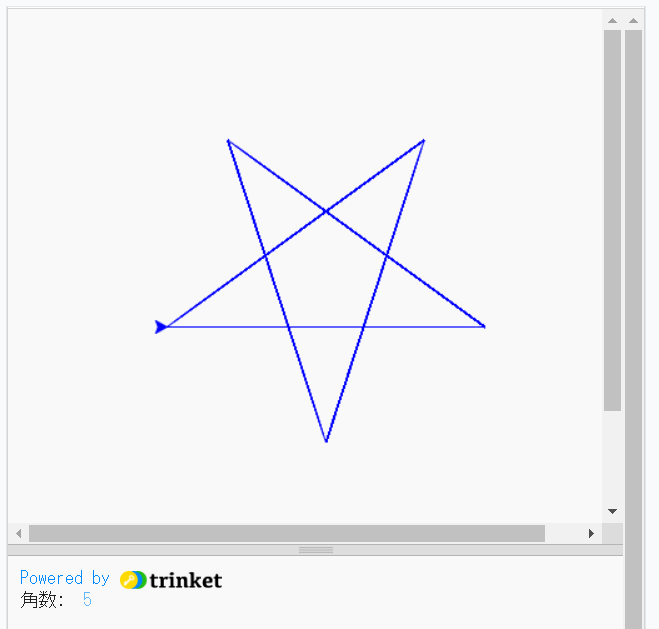
〔プログラム〕
プロジェクトファイル(プログラムファイル):右クリックでダウンロードして、EduBlocksで読み込むことにより実行できます。
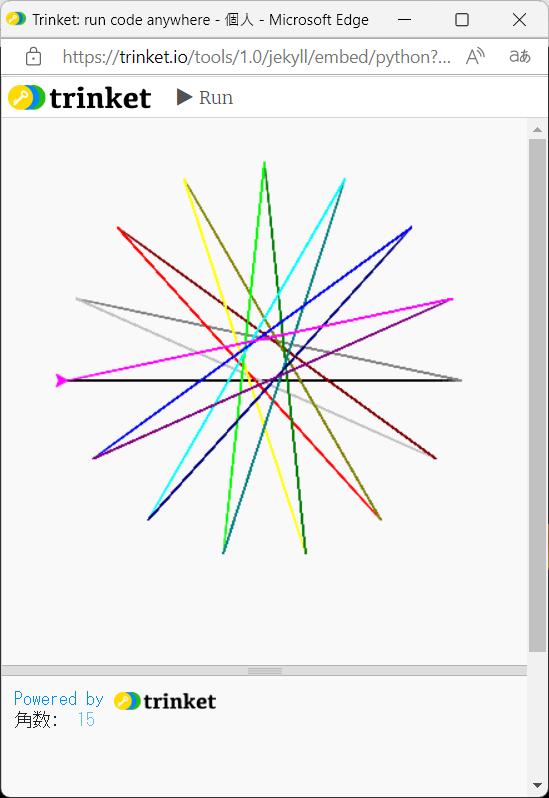
〔練習問題:描画例:15芒星〕※クリックすると動画を再生します。
〔技法〕Turtleグラフィックス、カラーコード
〔機能拡張版:N芒星の描画〕
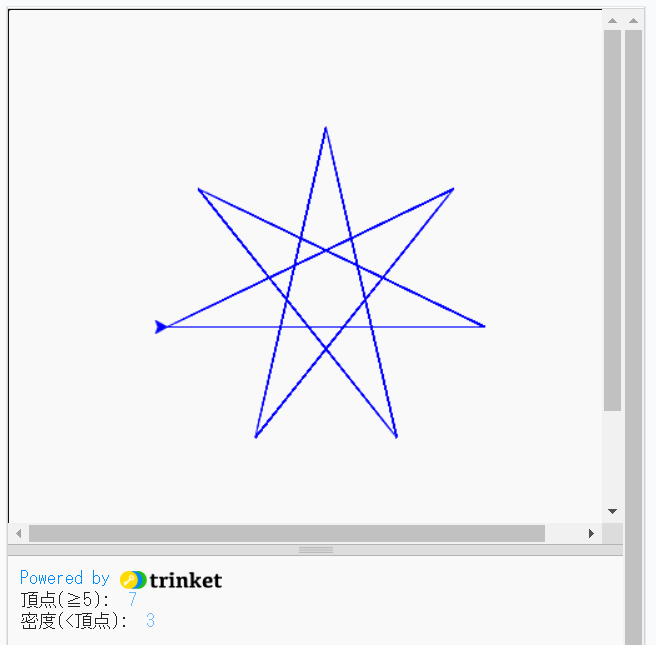
頂点の数n(≧5)と密度p(<頂点の数)を与えて描画します。ただし、3角関数を用いないアプローチのため複合星型正多角形は描画できません。
〔技法〕Turtleグラフィックス
〔実行例〕
〔プログラム〕
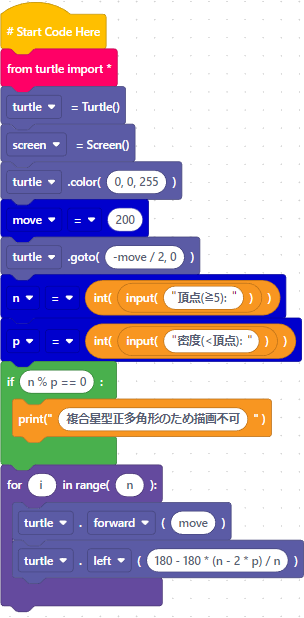
〔機能制限版:N芒星の描画〕
3角関数を用いてProcessingにより描画します。ただし、この版も複合星型正多角形は描画できません。
〔技法〕Processing、3角関数
〔実行例〕

〔プログラム〕

【練習問題】星型正n角形の描画
三角関数を用いてProcessingにより描画してください。ただし、この版では複合星型正n角形を含む任意の星型正n角形の描画に対応させます。
〔ヒント〕
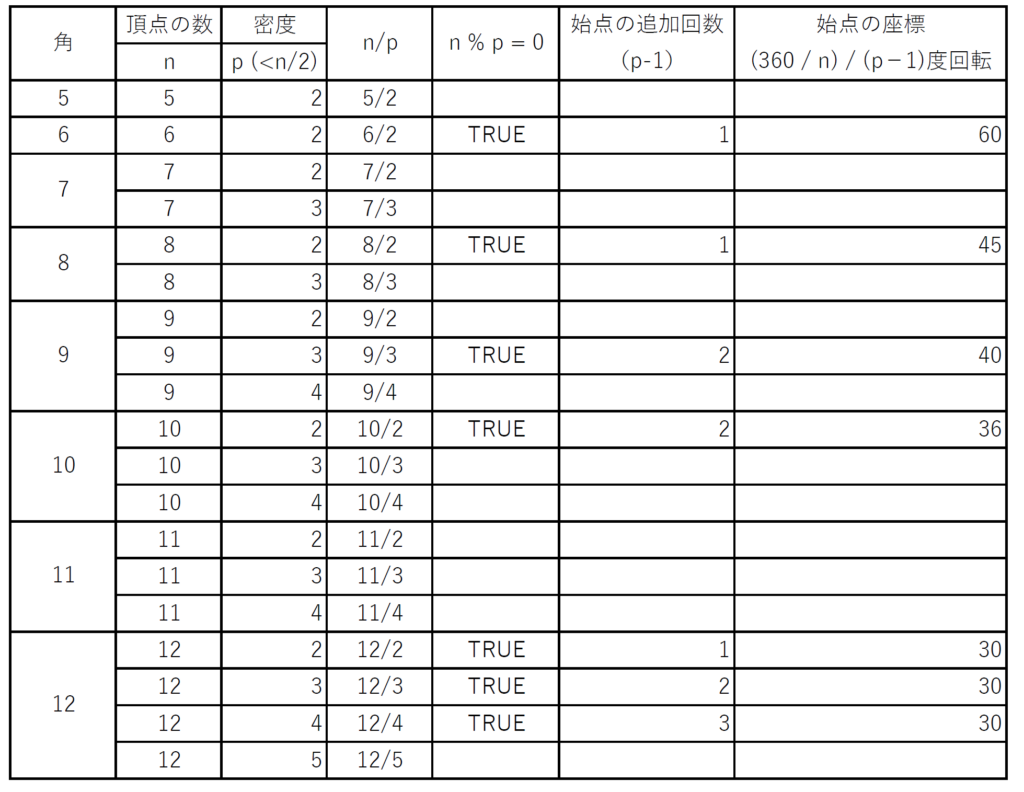
〔実行例〕

(3) カラーマップ
〔概要〕 カラーマップを描画し、クリックするとカラーコードを表示するプログラムです。
〔技法〕Processing、イベントドリブン
〔実行例〕
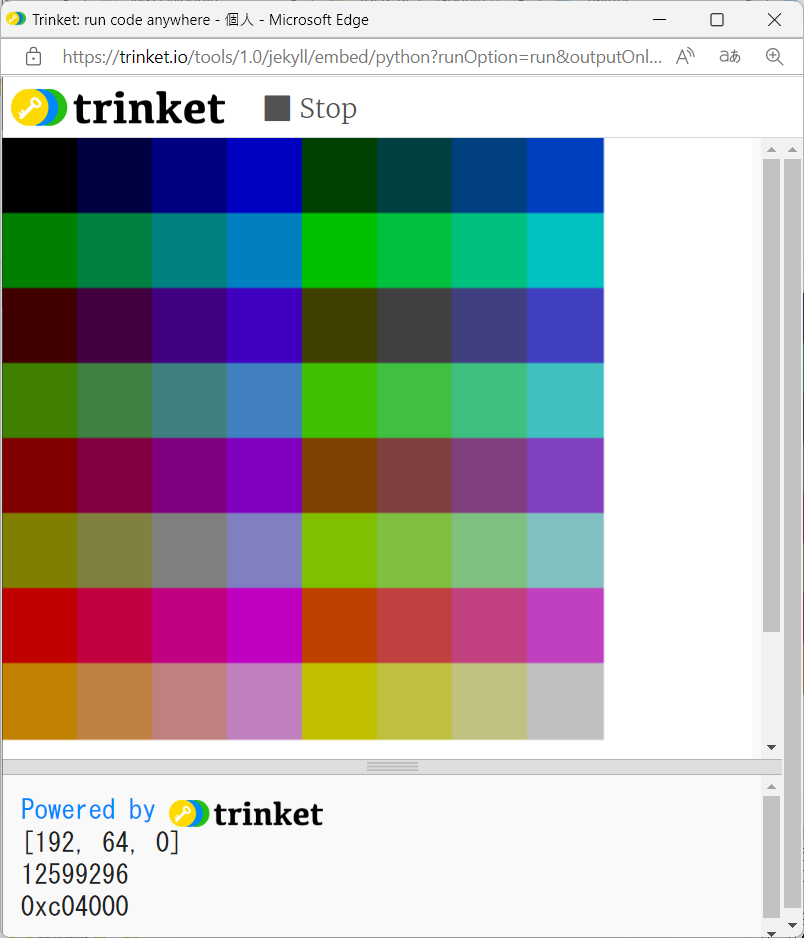
〔プログラム〕

プロジェクトファイル(プログラムファイル):右クリックでダウンロードして、EduBlocksで読み込むことにより実行できます。
(4)計算量
線形探索と2分探索の最大探索回数を比較する。
なお、EduBlocksでは、log2は、Numpy.log2()、math.log2()ともに実装されていないようなので、底の変換公式を用いて計算しています。
〔参考〕
Pythonでアルゴリズムに入門する! 押さえておきたい二分探索とバブルソートとは?
〔基本情報過去問〕
(a) 数値
〔実行例〕
.png)
〔プログラム〕
.json_.png)
(b) グラフ
〔実行例〕

〔プログラム〕

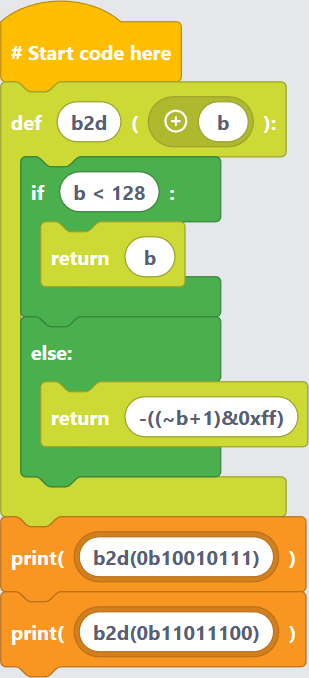
(5)1バイトの符号付整数を10進数に変換
〔実行例〕

〔プログラム〕
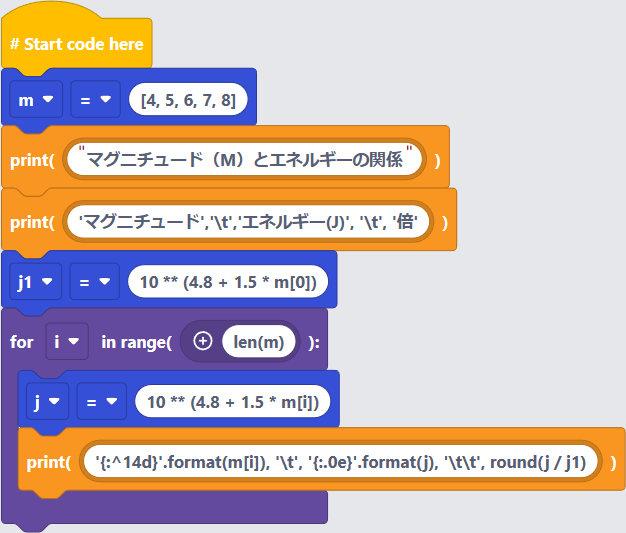
(6)マグニチュード(M)とエネルギーの関係
マグニチュード(M)とエネルギーの関係を表にします。ここでは、M4からM8まで1刻みとします。なお、M4を1とした場合の比も示します。
※能登半島地震をはじめとして、地震で被災された皆さまに心よりお見舞い申しあげます。
〔参考文献〕
〔技法〕リスト、反復、べき乗
〔実行例〕

〔プログラム〕
(7)余震の規模の変化
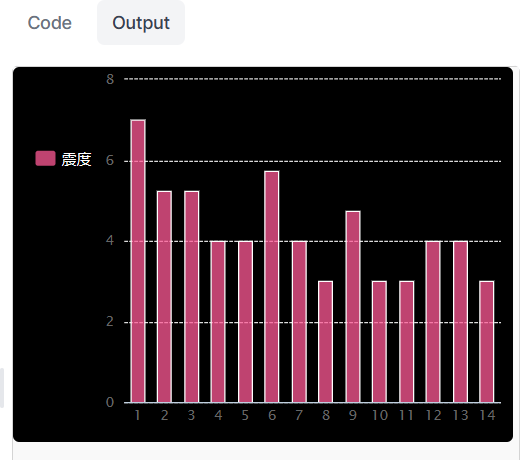
余震(大地震後の地震活動)の規模の変化をグラフで表示します。
表示は簡易的な方法で、大地震が発生した日を1日目として14日目までの期間を対象とします。また、1日単位を時間の区切りとして、その日の最大震度をデータとして使用します。また、震度の表示値は気象庁震度階級表を基に便宜的に次のように表現するものとします。
| 震度階級 | 計測震度 | 震度の表示値 |
| 4 | 3.5以上4.5未満 | 4 |
| 5弱 | 4.5以上5.0未満 | 4.75 |
| 5強 | 5.0以上5.5未満 | 5.25 |
| 6弱 | 5.5以上6.0未満 | 5.75 |
| 6強 | 6.0以上6.5未満 | 6.25 |
| 7 | 6.5以上 | 7 |
※能登半島地震で被災された皆さまに心よりお見舞い申しあげます。また、大地震後の地震活動(余震等)が早く収束することを祈念しています。
〔参考文献〕
〔技法〕リスト、pygal
〔実行例〕
〔プログラム〕

(8)余震の数の変化
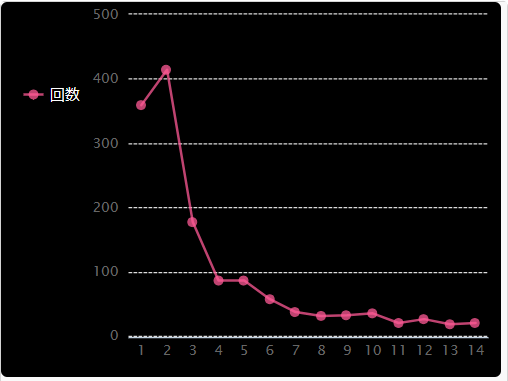
余震(大地震後の地震活動)の数の変化をグラフで表示します。
表示は簡易的な方法で、大地震が発生した日を1日目として14日目までの期間を対象とします。
※能登半島地震で被災された皆さまに心よりお見舞い申しあげます。また、大地震後の地震活動(余震等)が早く収束することを祈念しています。
〔参考文献〕
〔技法〕リスト、pygal
〔実行例〕
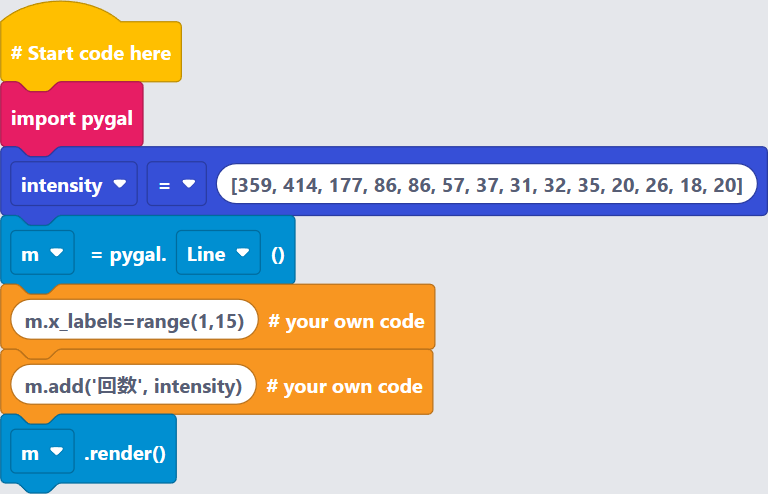
〔プログラム〕
【練習問題】
余震の数の変化を散布図として表示してください。また、回帰分析をしてください。
(9)都道府県名の略号
文字列処理の例として、都道府県名のローマ字の略号を生成します。
〔生成規則〕
- ヘボン式のローマ字で表現する。
- 先頭1文字は必ず使用する。
- 母音は削除し、子音のみ残す。
〔参考〕本格的な生成方法は、以下を参考にしてください。
〔技法〕リスト、文字列の連結、2重ループ
〔実行例〕
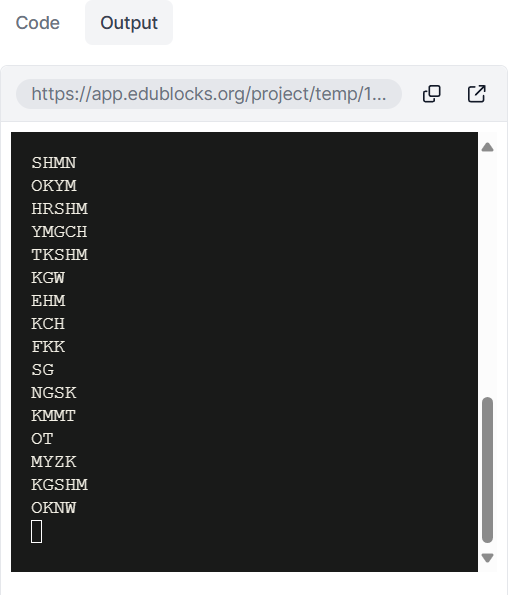
〔プログラム〕

(10) 織女星と牽牛星の距離
織女星と牽牛星との距離を余弦定理で求める。
〔参考〕
〔実行例〕
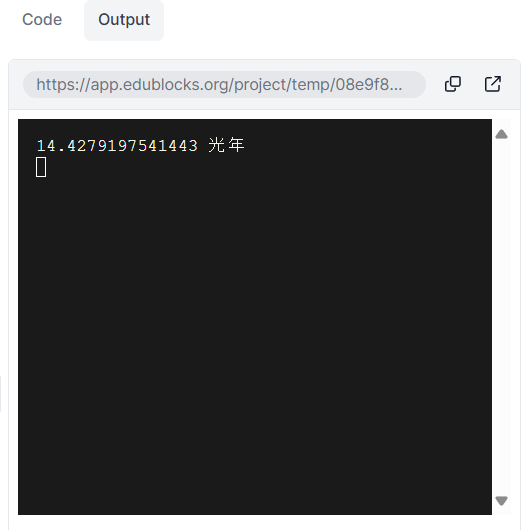
〔プログラム〕

(11) 座席位置の重心
〔参考〕
重量と重心位置:航空機の重量と重心位置の制限を遵守することは、飛行の安全性にとって重要である。
準備1
座席数が36の飛行機を考える。なお、座席はA~D列と前方からの番号1~9で表すものとする。
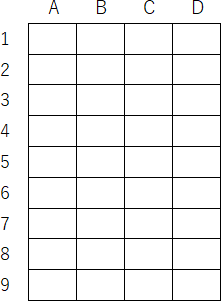
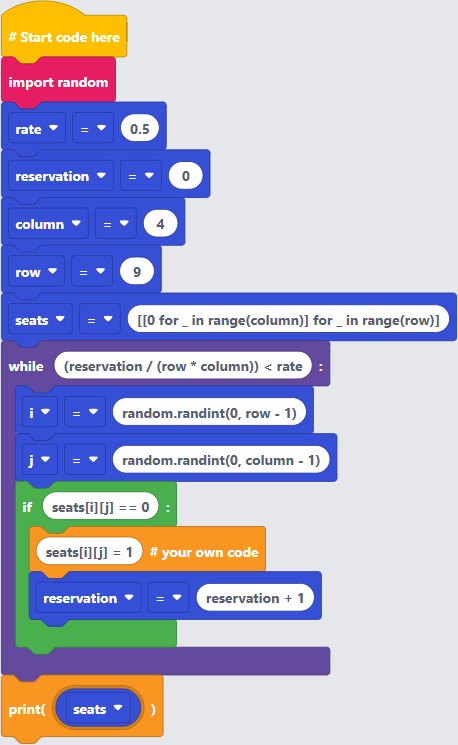
予約率が例えば50%を超えるまで、乱数で予約座席を配置するシミュレーションを行う。予約済みの座席位置を1、空き席を0で表すものとして、2次元リスト(配列)にデータを格納する。
〔技法〕乱数、2次元リスト(配列)、リストの内包表記、プライベート変数(高度)
〔実行例〕
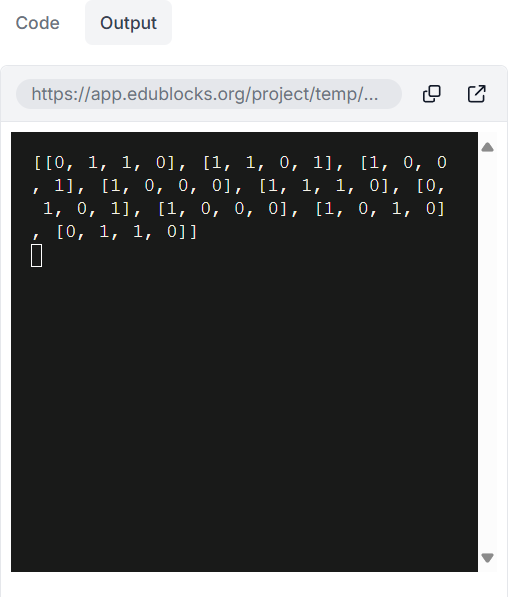
〔プログラム〕
練習問題1
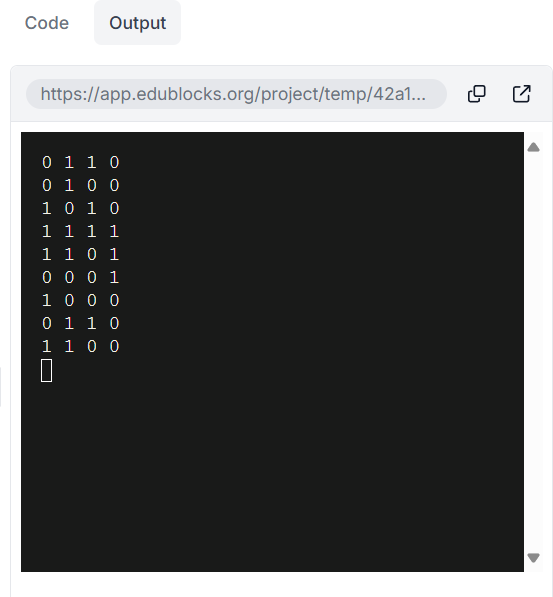
前項の「準備1」で生成したリストに基づいて、座席の空き状況(予約状況)を表示してください。予約済みの座席位置を1、空き席を0で表すものとする。
〔実行例〕
〔プログラム〕
(省略)
練習問題2
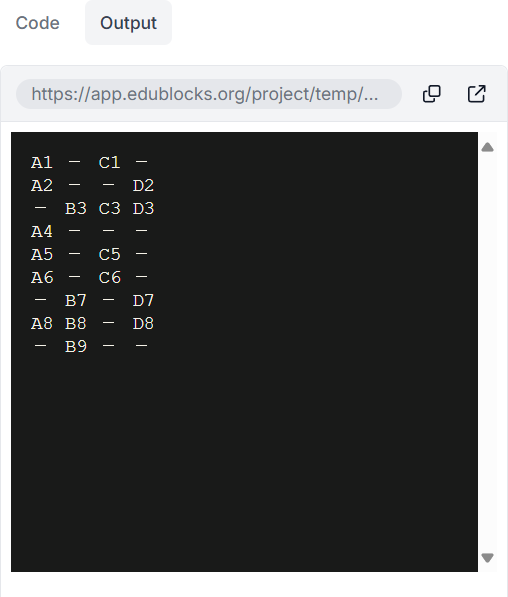
前項の「練習問題1」と同様に座席の空き状況(予約状況)を表示するが、予約済みの座席位置を座席番号(例:A1)、空き席を「ー」で表すものとする。
〔実行例〕
〔プログラム〕
(省略)
主題
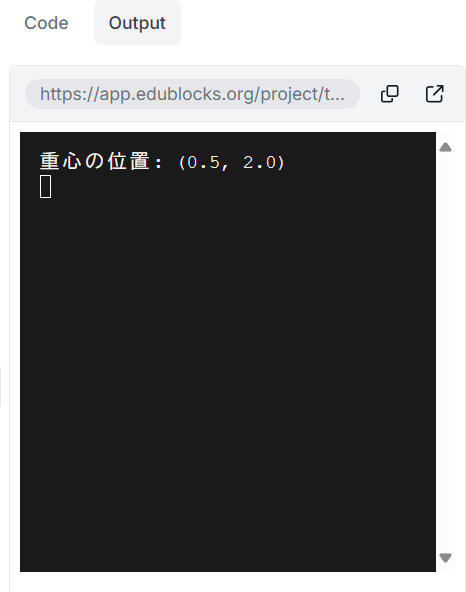
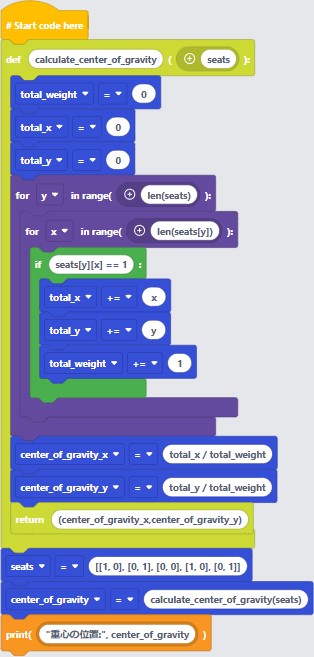
予約座席位置のリスト(2次元配列)を読み込んで座席位置の重心を求める。ただし、A1の位置を座標原点(0, 0)とする。また、座席位置の右方向をxの増加、下方向をyの増加とする。
〔実行例〕
〔プログラム〕
練習問題3
乱数を用いて予約座席位置のリスト(2次元配列)を生成し、重心位置を繰り返し求めるシミュレーションを行い、その平均を求めてください。
〔実行例〕
(省略)
〔プログラム〕
(省略)
(12)南海トラフ地震の発生間隔の平均
次図に基づく計算です。ただし、ほぼ同時に起きた地震については後発年を採用します。
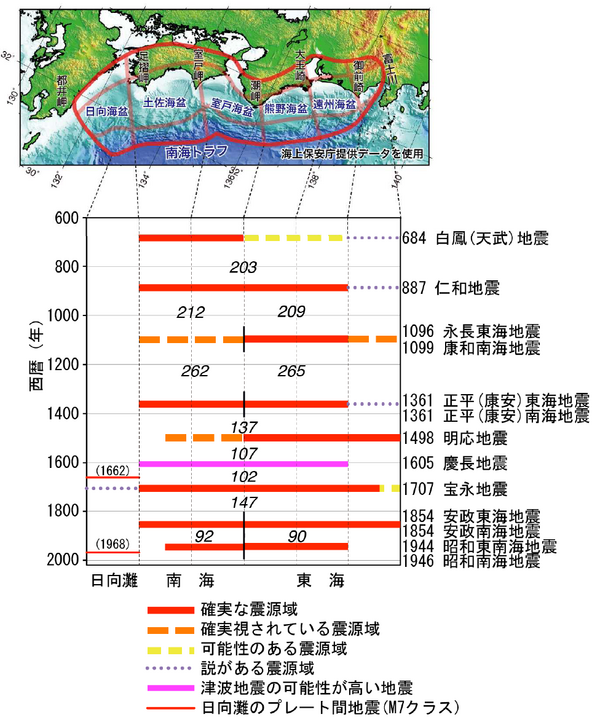
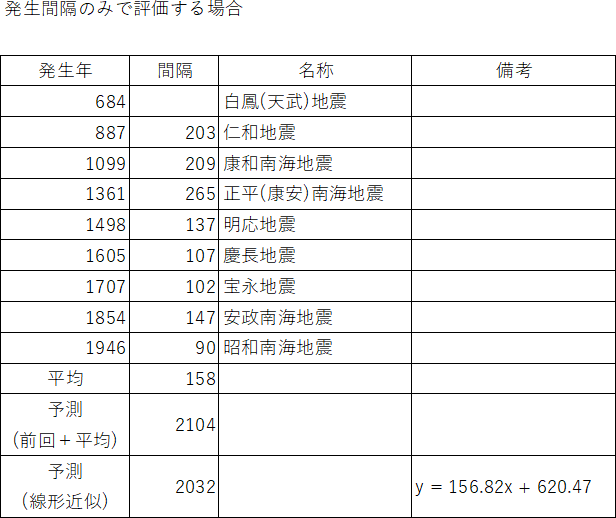
※地震の被害に遭われたすべての方々にお見舞い申しあげるとともに、将来の地震被害が少ないことを祈念いたします。
〔技法〕リスト、pygal
〔実行例〕
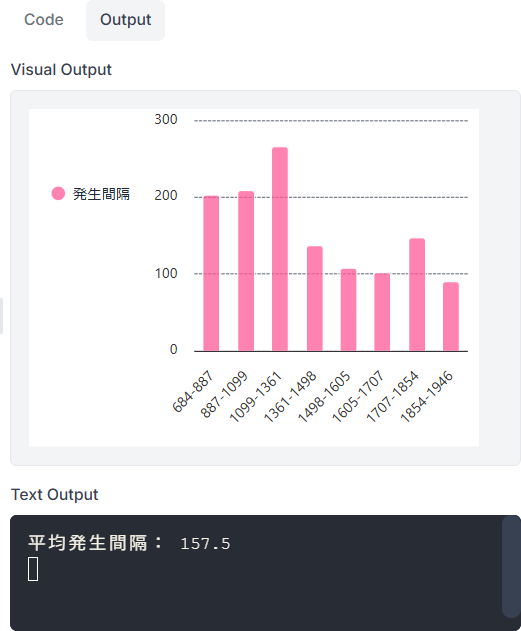
〔プログラム〕
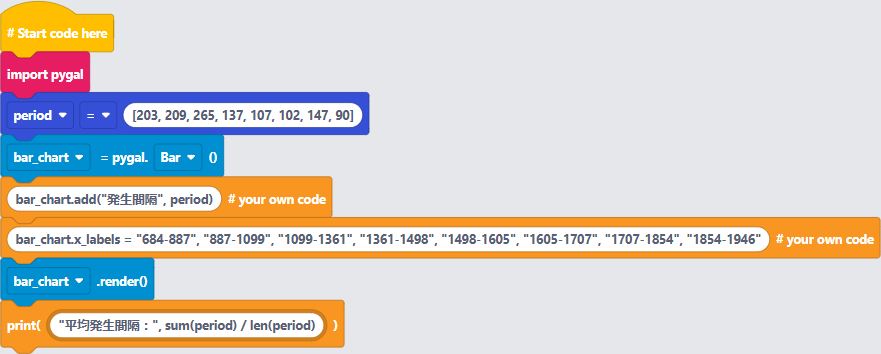
練習問題
発生年を元データとして、発生間隔およびラベルも生成してください。
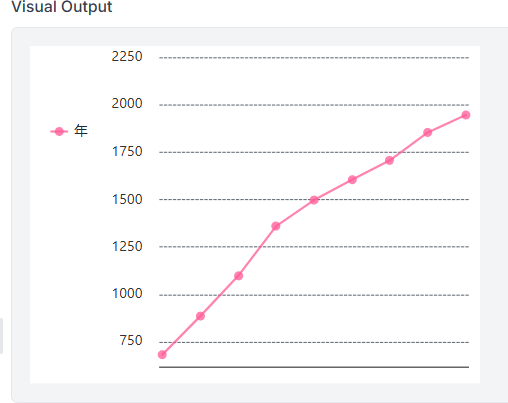
(13)南海トラフ地震の発生年の折れ線グラフ
※地震の被害に遭われたすべての方々にお見舞い申しあげるとともに、将来の地震被害が少ないことを祈念いたします。
〔技法〕リスト、pygal
〔実行例〕
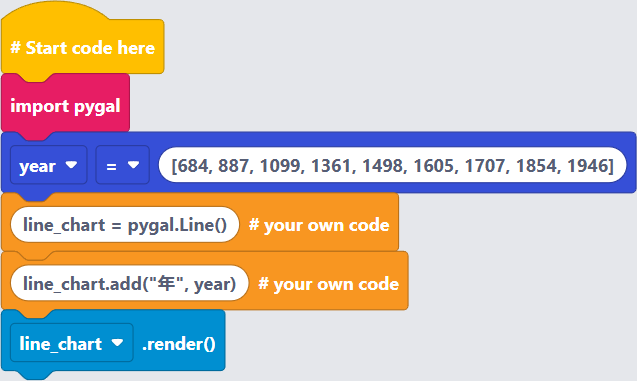
〔プログラム〕
練習問題
x軸ラベルに、白鳳、仁和、康和、…のように、地震名を表示してください。
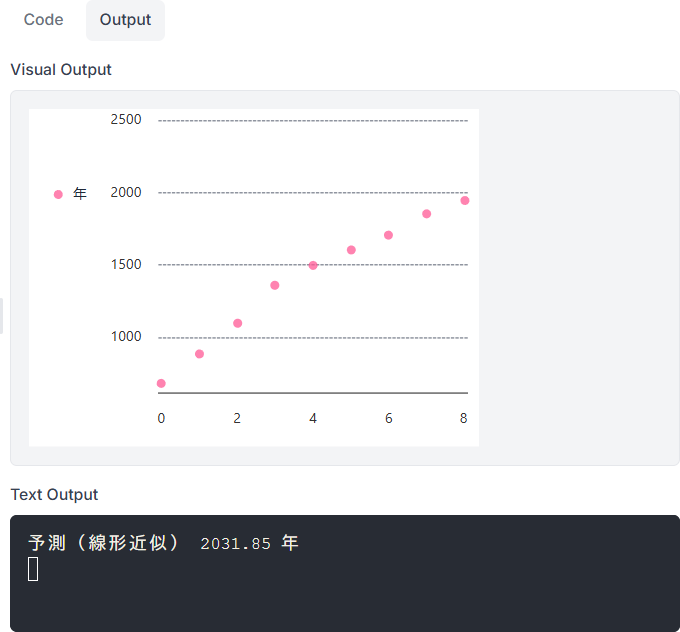
(14)南海トラフ地震の回帰分析
最も単純な「発生間隔のみで評価する」モデルによる回帰分析(線形近似)です。
回帰直線は、あらかじめこちらの方法で求めておきます。
EduBlocksのPygalでは複数のグラフを重ねることができないようなので、散布図のみ表示します。
※地震の被害に遭われたすべての方々にお見舞い申しあげるとともに、将来の地震被害が少ないことを祈念いたします。
〔技法〕リスト、pygal
〔実行例〕
〔プログラム〕

練習問題
Pyplotで散布図と回帰直線のグラフィック表示をしてください。
(15)URLエンコード・デコード
〔実行例〕
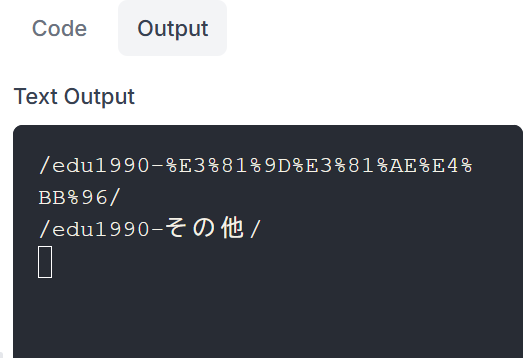
〔プログラム〕

(16)キーボードからの繰返し入力
キーボードからデータを入力して表示する処理を繰り返す。なお、[Enter]キーのみが入力されたら繰返しを終了するものとする。
(a) 方法1:先読み
〔技法〕input()、空文字列
〔実行例〕
〔プログラム〕
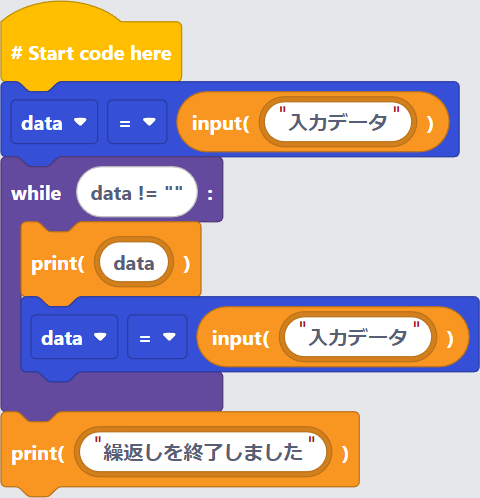
練習問題
数字データを入力して数値データに変換して表示してください。
(b) 方法2:無限ループ
〔技法〕input()、無限ループ
〔実行例〕
〔プログラム〕
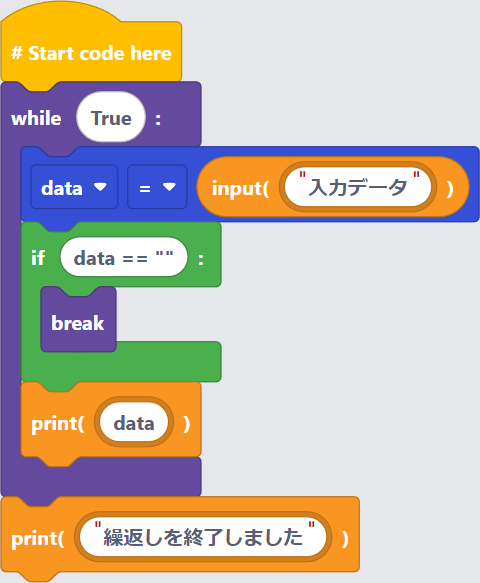
練習問題
数字データを入力して数値データに変換して表示してください。
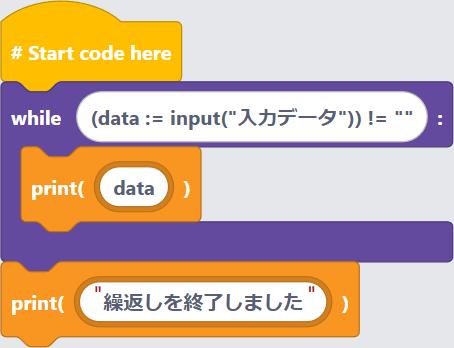
(c) 方法3:ウォルラス演算子
〔環境〕Python3.8以降
〔技法〕walrus
〔実行例〕

〔プログラム〕
練習問題
数字データを入力して数値データに変換して表示してください。
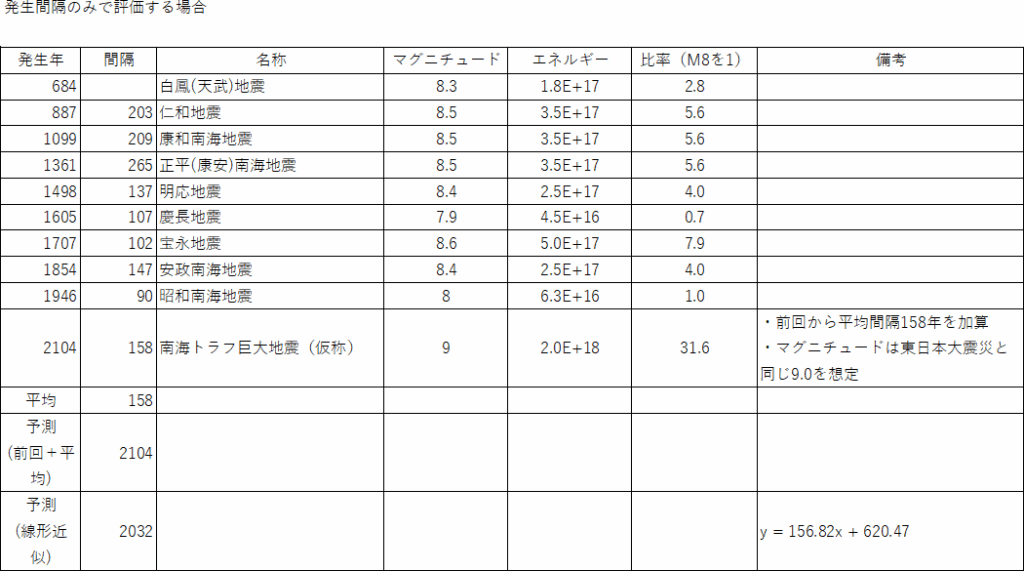
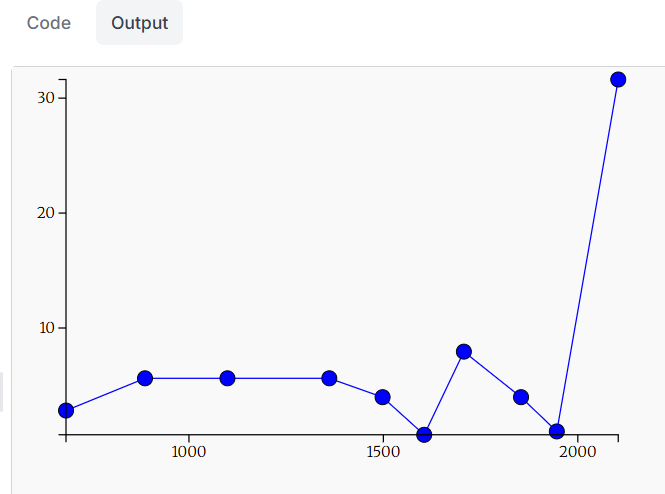
(17)南海トラフ地震のエネルギー比較
マグニチュードM8を1とした時の南海トラフ地震のエネルギー比較をグラフ表示する。
(仮定)
- 次に起こると予想されている地震の発生年は前回の発生年に平均間隔158年を加算する。
- 南海トラフ巨大地震(仮称)のマグニチュードは東日本大震災と同じ9.0を想定する。
※地震の被害に遭われたすべての方々にお見舞い申しあげるとともに、将来の地震被害が少ないことを祈念いたします。
〔環境〕July 2023バージョン
〔関連〕
〔技法〕リスト
〔実行例〕
〔プログラム〕

Copyright (C) 2022 Easy Programming
