py1060 – データの前処理

〔概要〕データの前処理の例です。

　Pythonによる前処理（奇数列の抽出）の例はPy1030で紹介しました。

　この例ではExcelで手動で前処理した結果を利用します。例として、宮崎県内のアメダス観測地点の気温と標高との関係を調べてみます。また、重回帰分析への発展として、説明変数を緯度と標高、目的変数を気温にして試してみます。

〔技法〕Excel（手動）、単回帰分析、重回帰分析

---

＜単回帰分析＞

【Excel】

　Py1030で紹介したアメダスの観測地点の、標高のデータを取得してExcelで整形してみます。

1. 地域気象観測システム（アメダス）のページから地域気象観測所一覧 [ZIP圧縮形式]をダウンロードします。
   
   
2. ダウンロードしたファイルを解凍すると、たとえば「ame_master_20211207.csv」のようなデータが取得できます。
   

都府県振興局,観測所番号,種類,観測所名,ｶﾀｶﾅ名,所在地,緯度(度),緯度(分),経度(度),経度(分),海面上の高さ(ｍ),風速計の高さ(ｍ),温度計の高さ(ｍ),観測開始年月日,備考1,備考2
宗谷,11001,四,宗谷岬,ｿｳﾔﾐｻｷ,稚内市宗谷岬,45,31.2,141,56.1,26,10.1,1.5,昭53.10.30,－,－
宗谷,11016,官,稚内,ﾜｯｶﾅｲ,稚内市開運　稚内地方気象台,45,24.9,141,40.7,3,24.1,－,#昭50.4.1,11903,－
宗谷,11046,四,礼文,ﾚﾌﾞﾝ,礼文郡礼文町大字香深村トンナイ,45,18.3,141,2.7,65,10,1.5,平15.10.17,－,－
　（以下省略）

3. このCSV形式のファイルを読み込んでExcel形式に変換します。
   
   
   
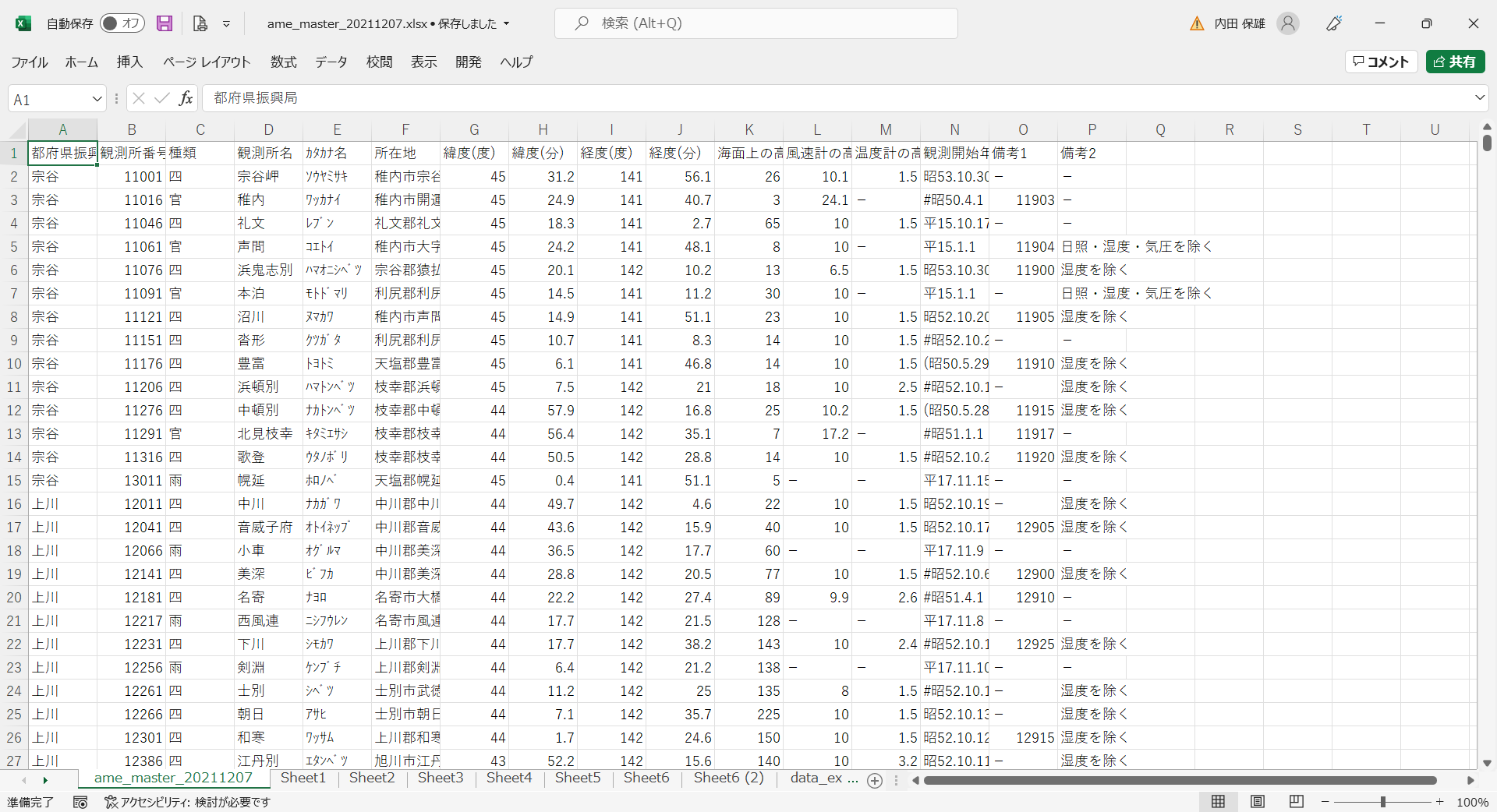
4. 現在のワークシートをコピーして、新しいワークシートたとえば「Sheet1」に貼り付けます。そして、メニューから[ホーム]→[並べ替えとフィルター]→[フィルター]を選択してから、たとえば「宮崎」のみを選択します。そして、たとえば「Sheet2」に貼り付けます。
   
   
   
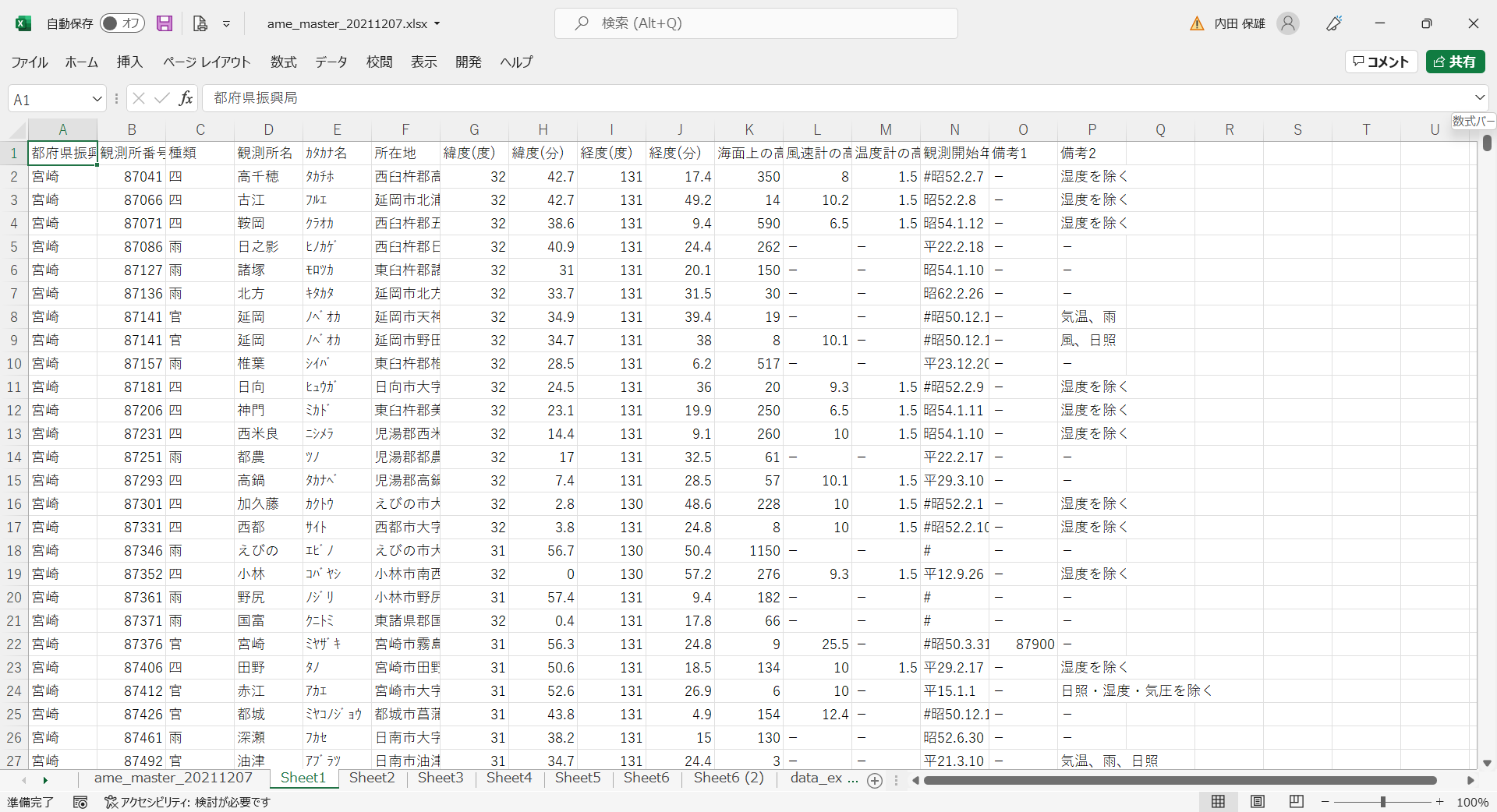
5. その内容を確認すると、観測所名の「延岡」と「油津」が重複しています。備考２を見て、気温に関係しない方の行を削除します。そして、たとえば「Sheet3」に貼り付けます。
   
   
   
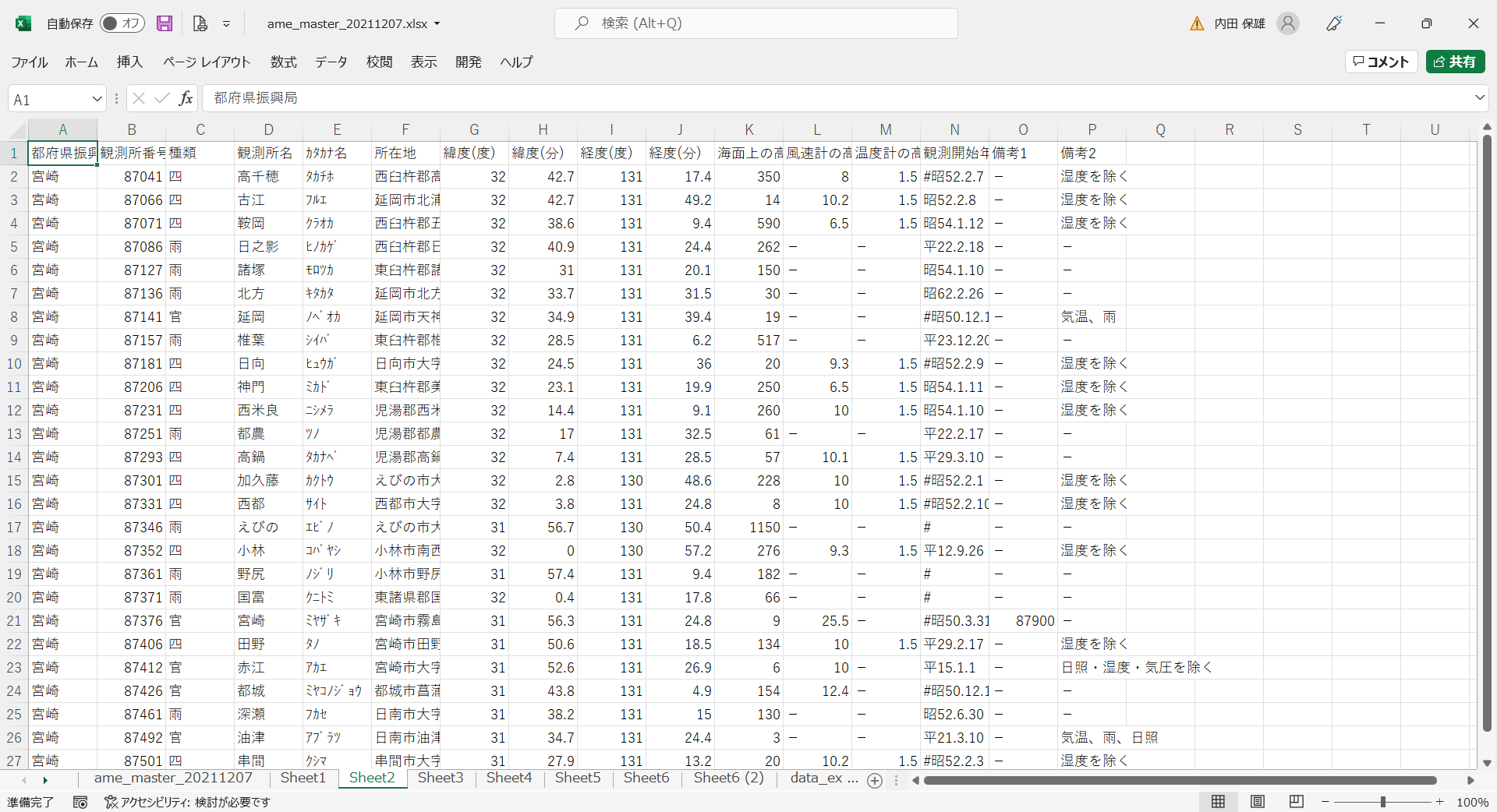
6. 観測所名、海面上の高さ(ｍ)以外の列を削除します。すると以下のようになります。
   
   
   
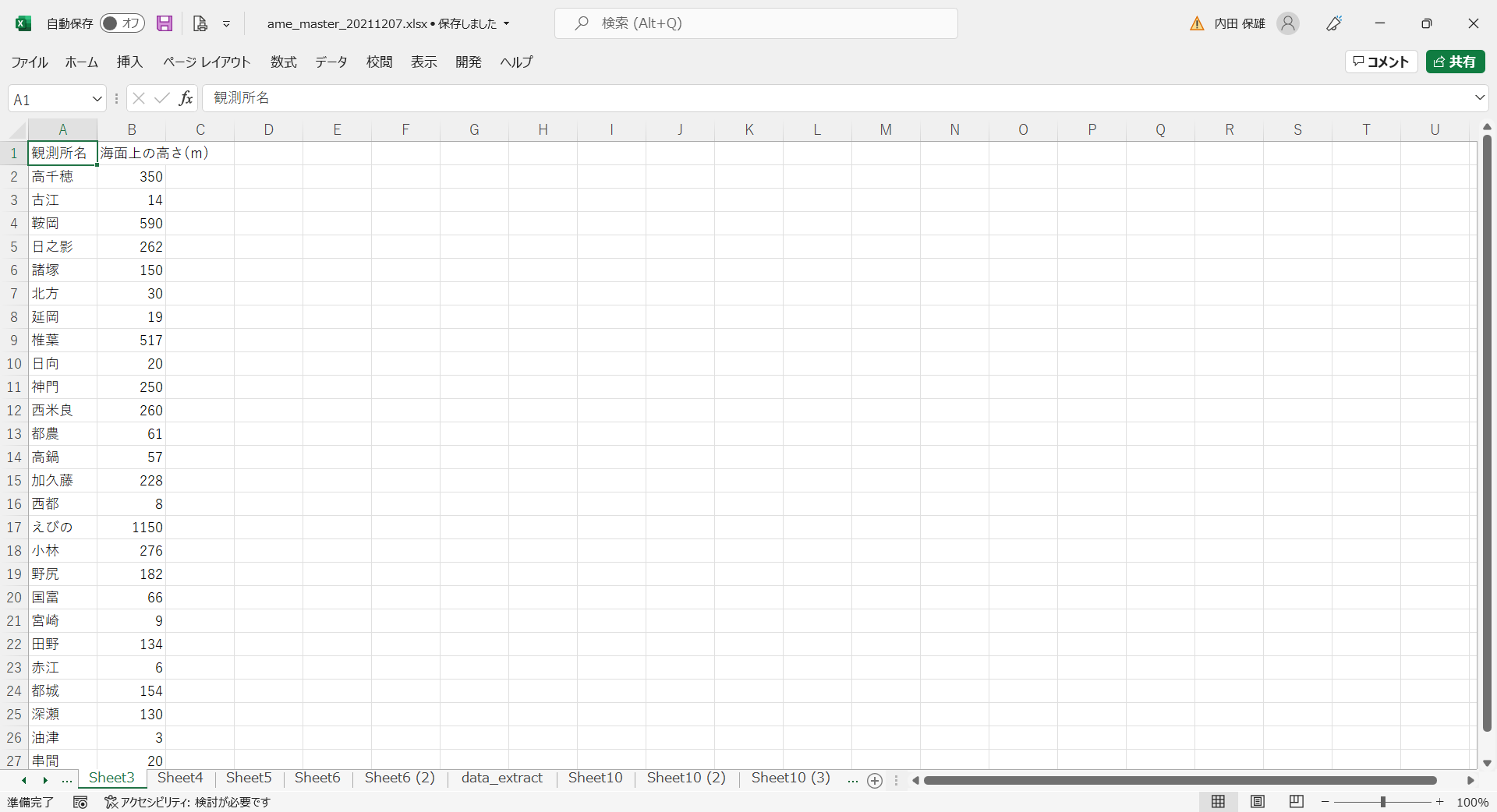
7. Py1030で作成した「data_extract.csv」のデータを新しいシートに貼り付けて、すべてのデータをコピーします。
   
   
   
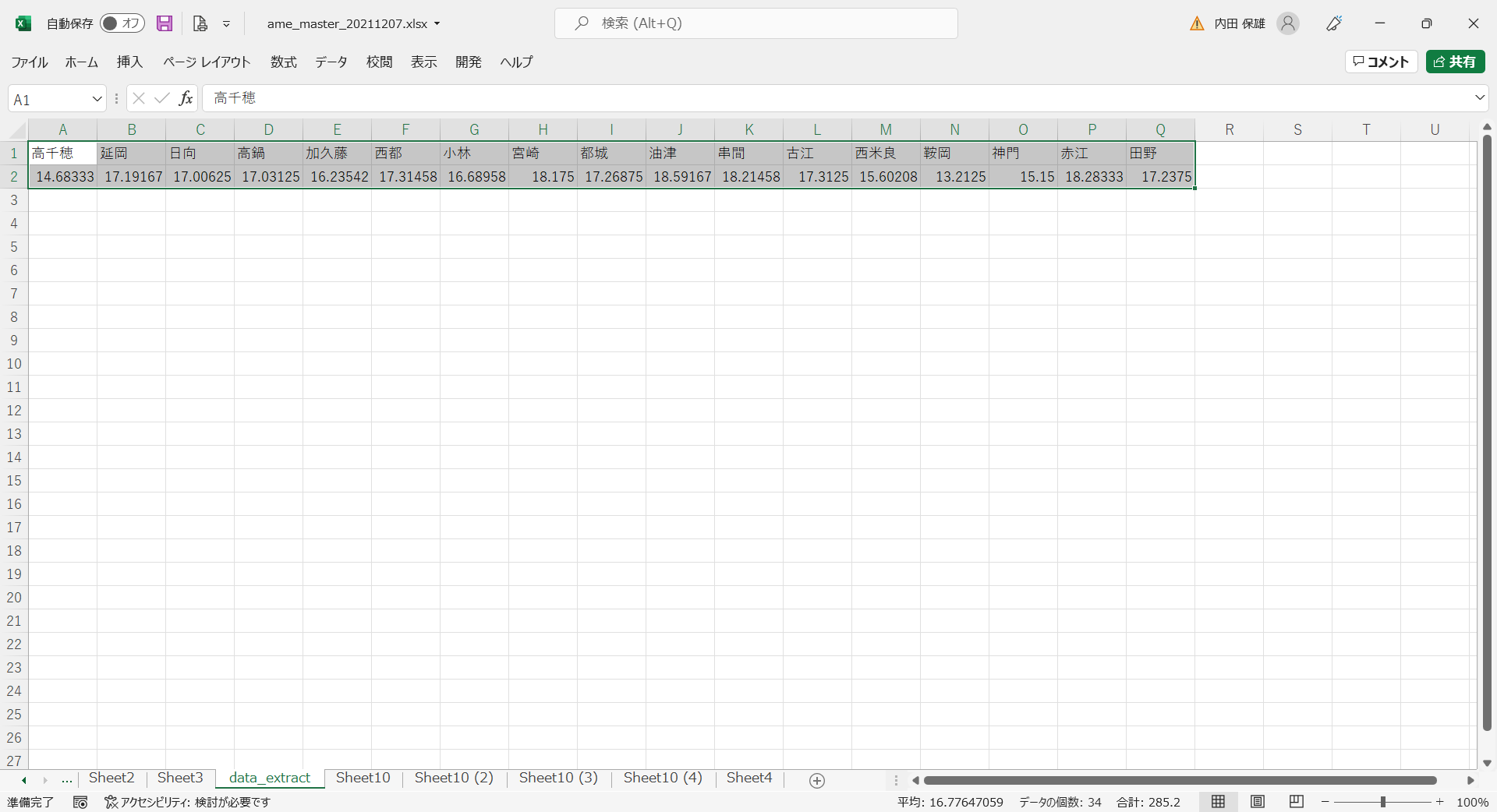
8. 新しいシートを追加してから、A1セルを右クリックして、メニューから[形式を選択して貼り付け]を選択します。
   
   
   
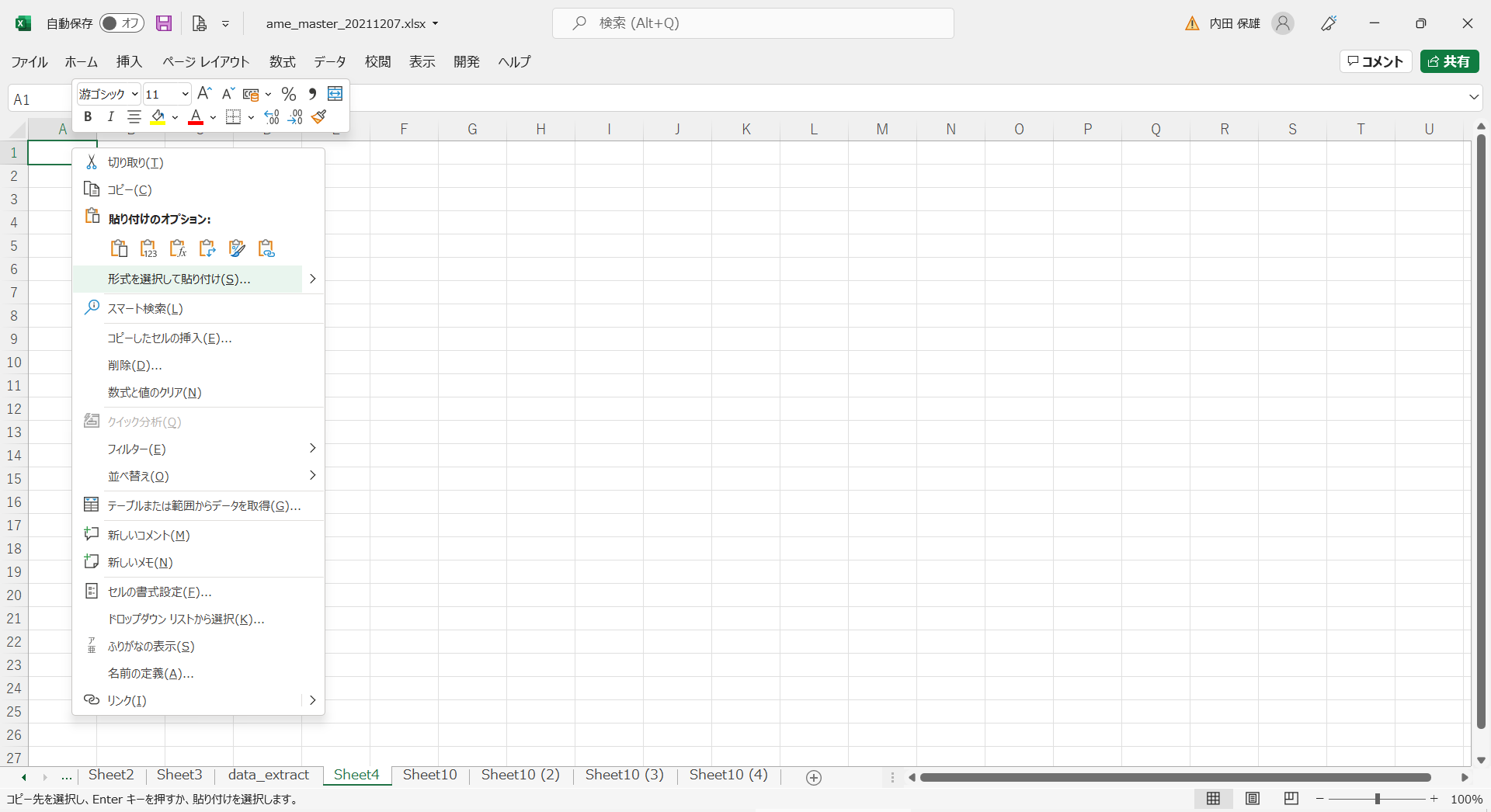
9. [形式を選択して貼り付け]ダイアログボックスで[行/列の入れ替え]にチェックをいれて[OK]をクリックします。
   
   
   
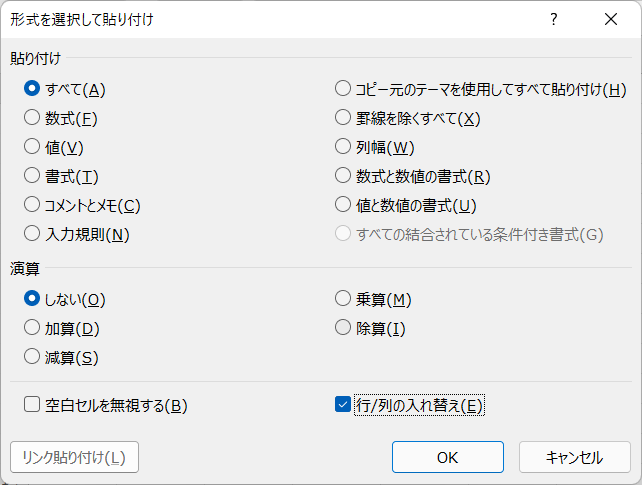
10. 行と列とが入れ替って貼り付けられます。
    
    
    
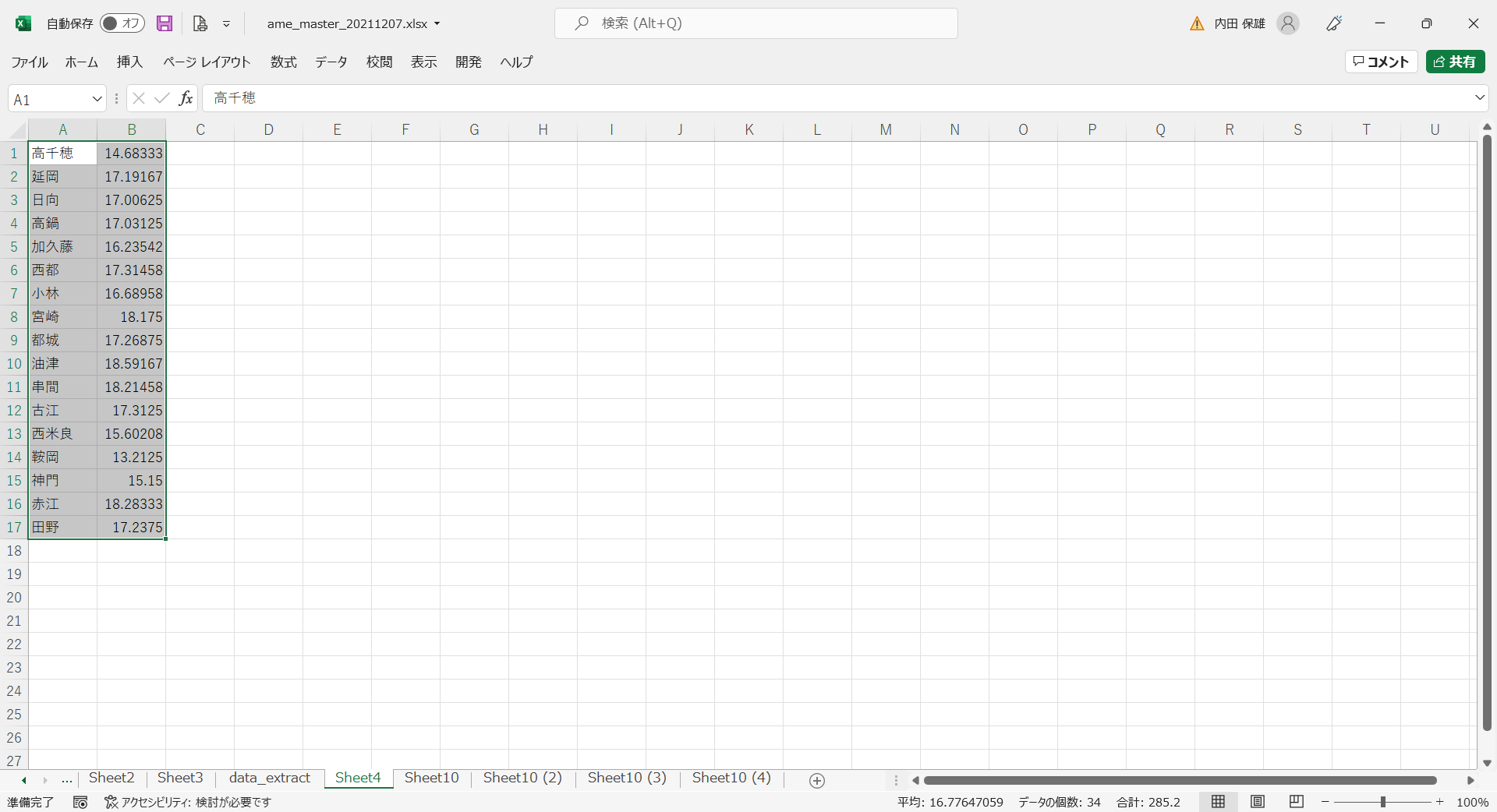
11. メニューから[ホーム]→[並べ替えとフィルター]→[昇順]を選択して、観測地点名の昇順に並べ替えます。先頭が「鞍岡」になります。
    
    
    
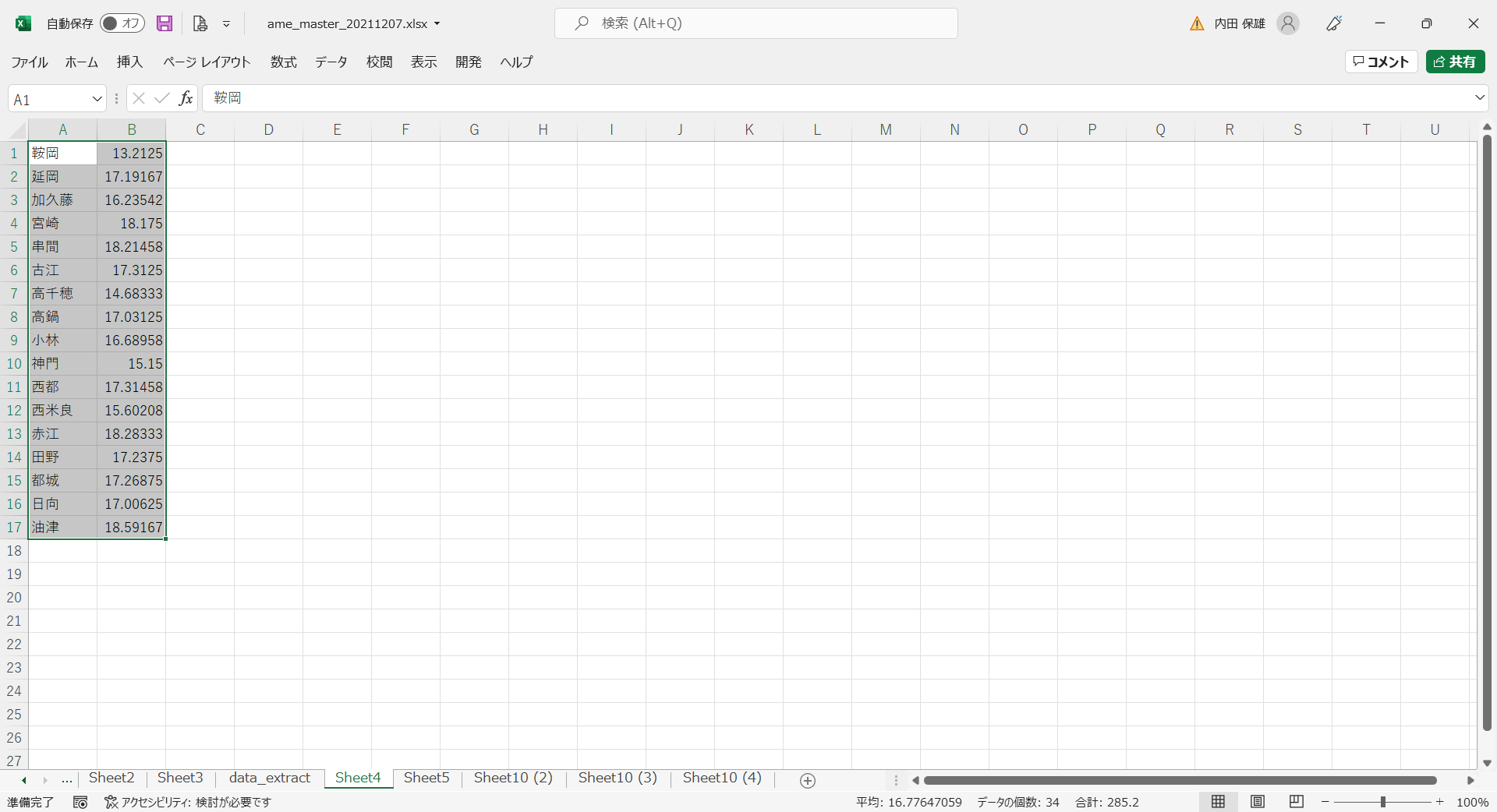
12. Sheet3の標高のデータをコピーして次の図のように貼り付けます。
    
    
    
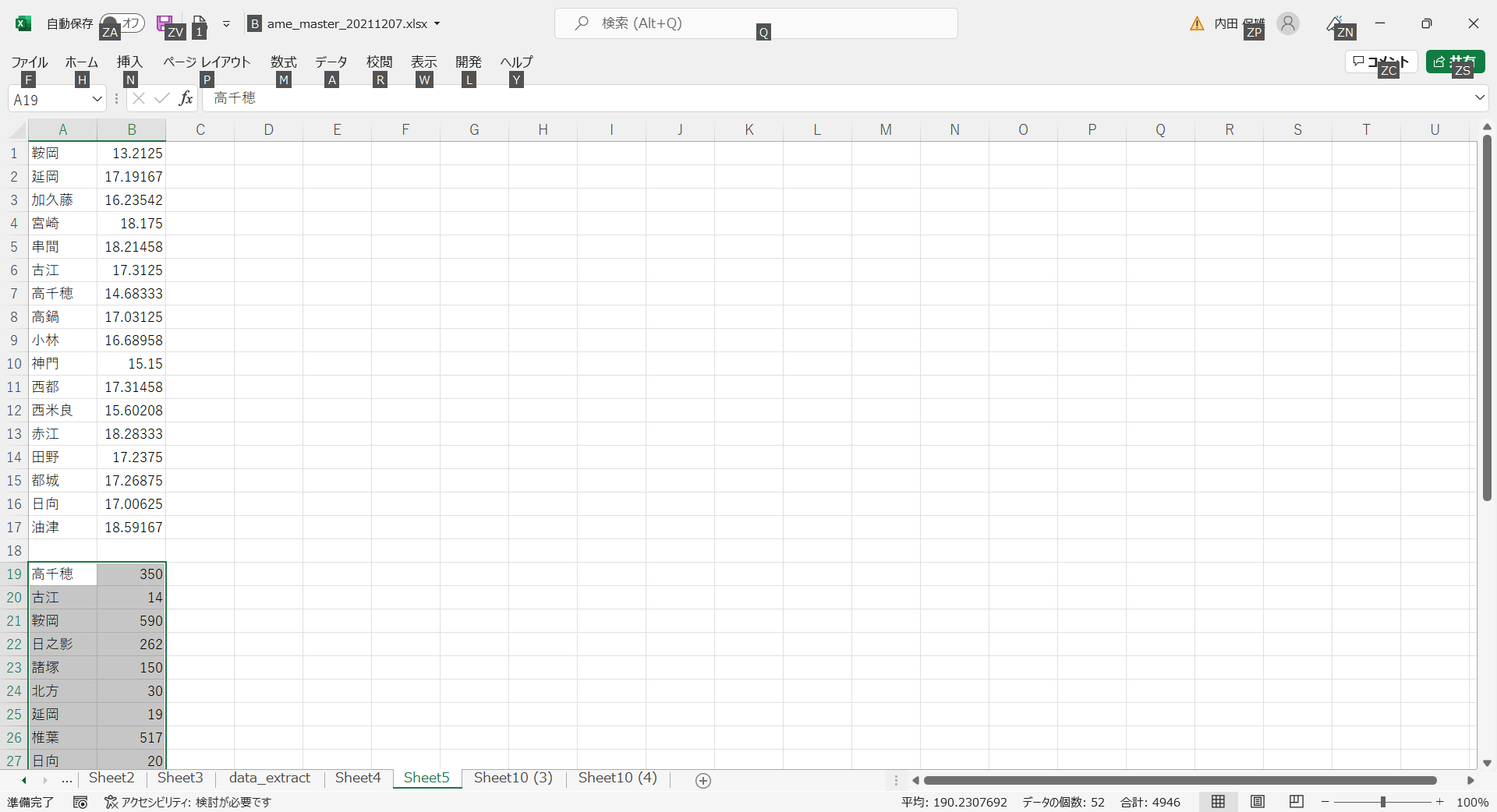
13. その後、前項と同様に並べ替えます。並べ替える理由は、次の処理で表引き（VLOOKUP）をおこなうための準備です。
    
    
14. C1セルに「=VLOOKUP(A1,$A$20:$B$45,2)」と入力し、「油津」までコピーします。
    
    
    
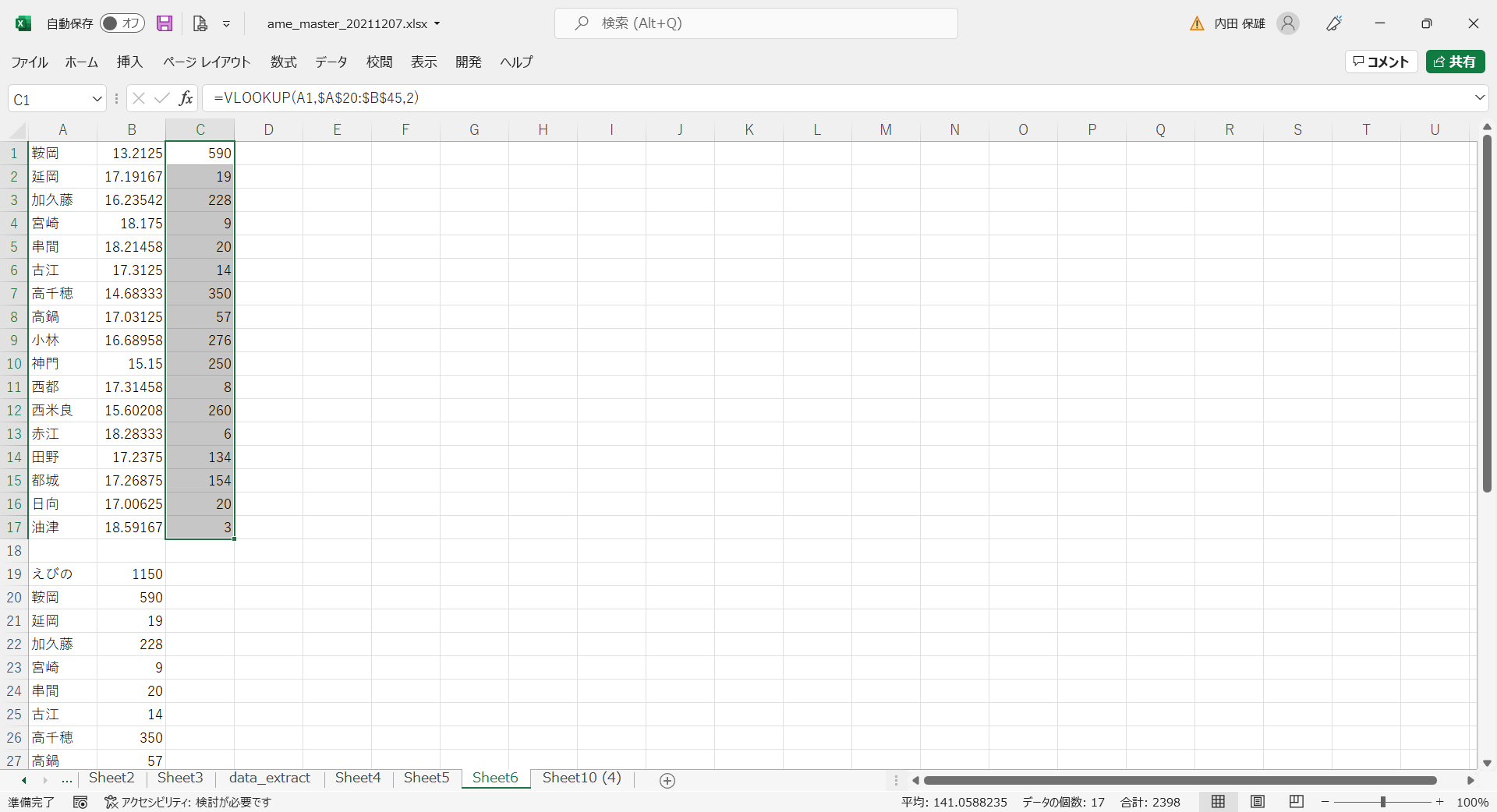
15. これで、観測地点名、平均気温、標高のデータが並びました。
    
    
16. 平均気温と標高のデータを入れ替えます。その理由は、横軸を標高（説明変数）、縦軸を平均気温（目的変数）として表示するためです。
    
    
    
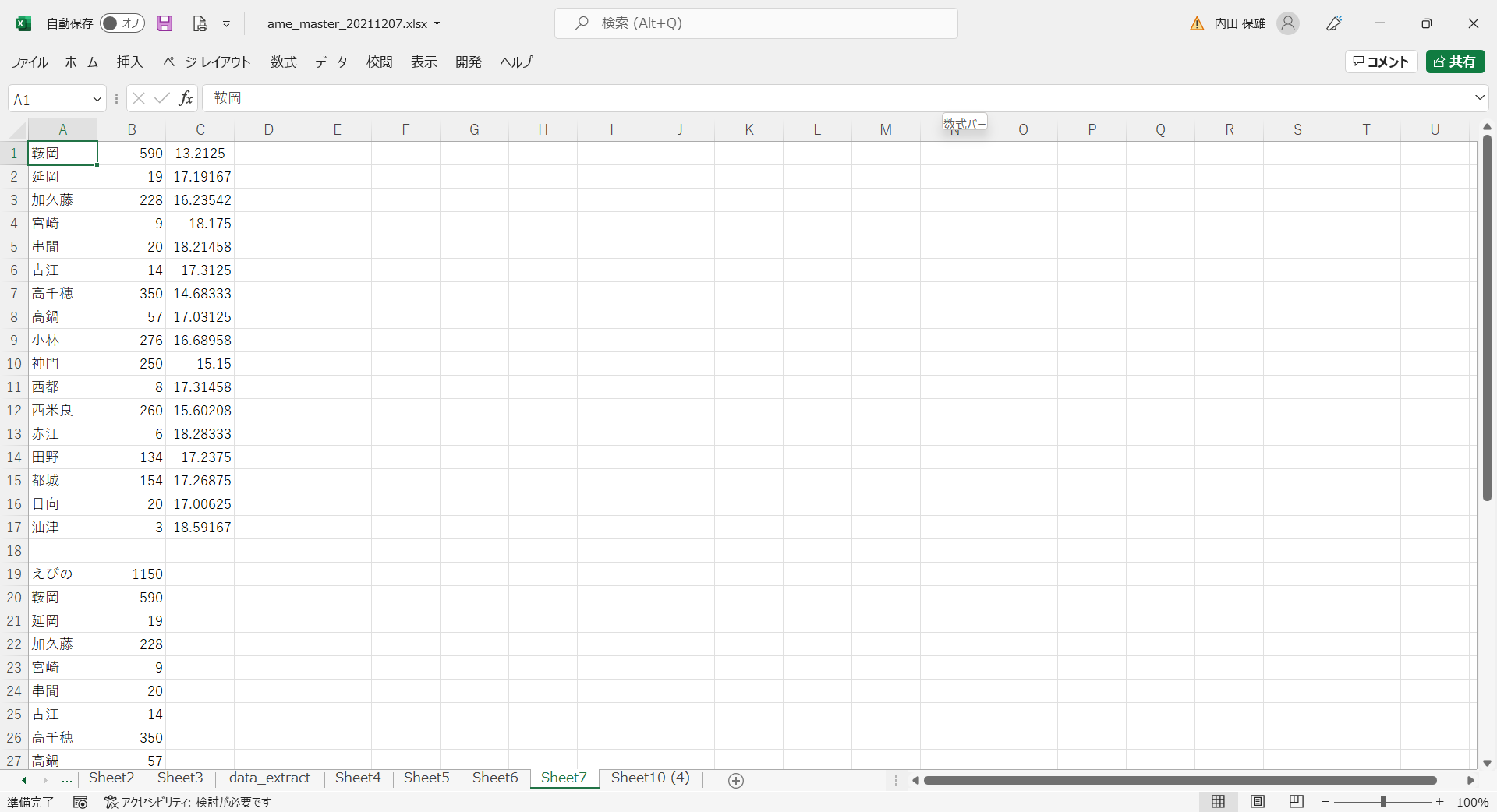
17. Py1010と同様にして、散布図と回帰式を表示します。
    
    
    
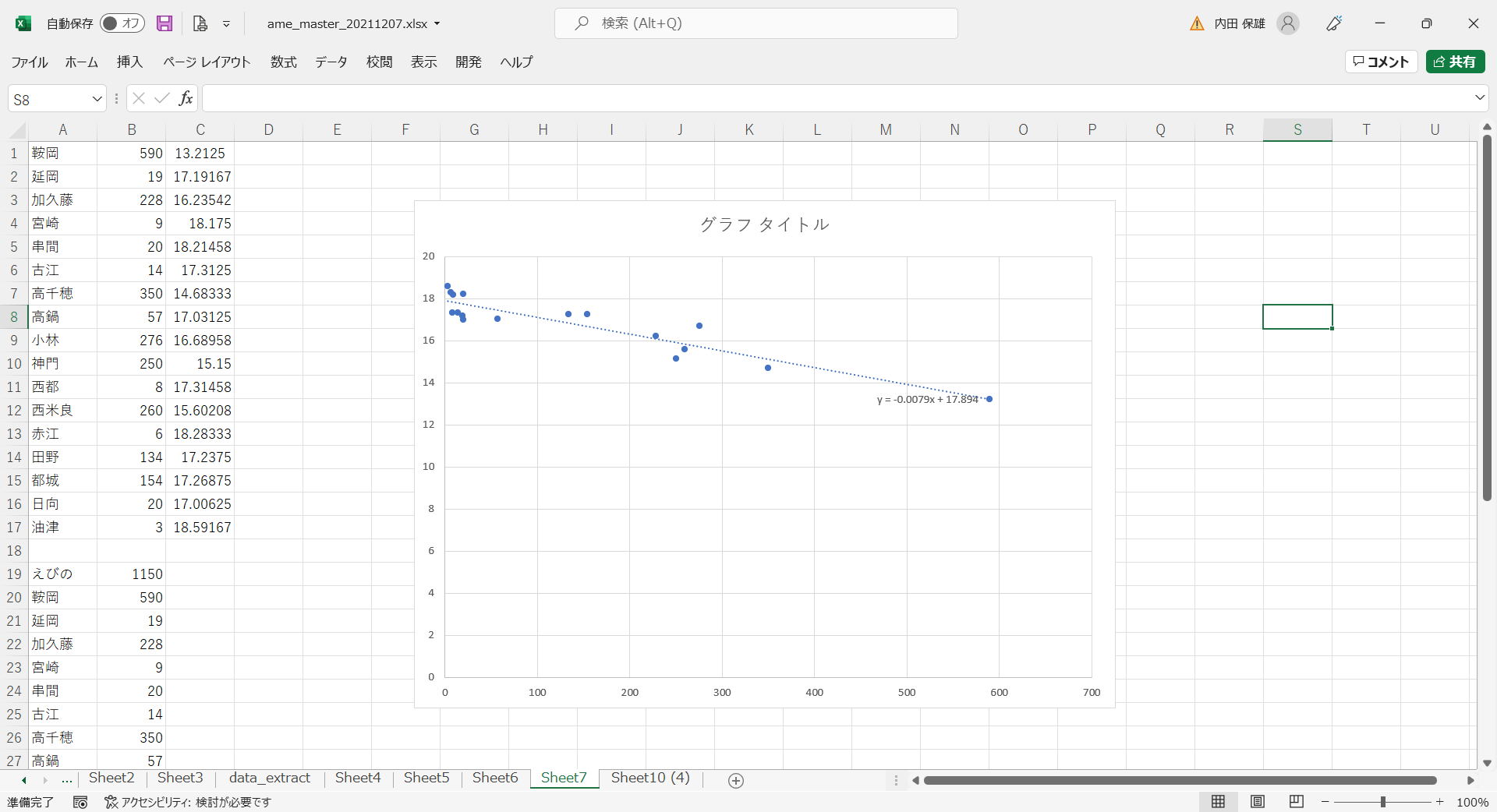
18. 回帰式は「y = -0.0079x + 17.894」となりました。つまり、標高が100m上がると0.79度気温が下がるということです。一般的には「標高が100m高くなると気温は約0.65℃下がる」とされていますが、今回は狭い範囲での少ないデータで試したのでこのような結果となりました。
    

【Python】

　前処理したデータを用いて、Pythonで単回帰分析を行うと以下のようになります。

〔データ〕

　Excelで前処理したデータに「x」と「y」の見出しを付けてから、CSV形式で、たとえば「data.csv」という名前で保存しておきます。

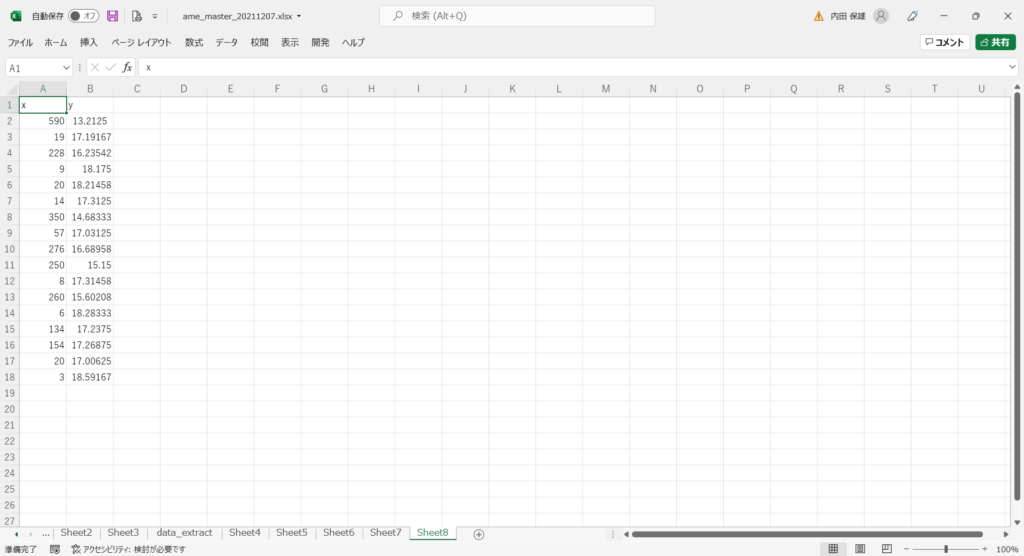
〔実行例〕

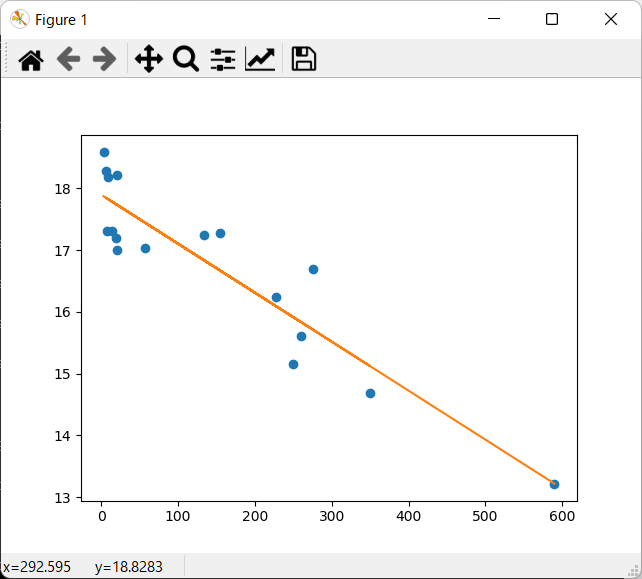
　コマンドラインに、次のように回帰変数と切片が表示されます。Excelの結果と一致していることが確認できます。

[[-0.00792186]]
[17.89391898]

〔プログラム〕

　py1010とほぼ同じプログラムです。

import pandas as pd
import matplotlib.pyplot as plt
from sklearn import linear_model

df = pd.read_csv('data.csv')

x = df[['x']]
y = df[['y']]

model = linear_model.LinearRegression()
model.fit(x, y)
print(model.coef_)
print(model.intercept_)

# グラフ表示
plt.plot(x,y,'o')
plt.plot(x,model.predict(x))
plt.show()

• 参考資料
  • sklearn
  • linear_model
  • LinearRegression

---

＜重回帰分析＞

　発展として重回帰分析の結果のみを示します。

〔データ〕

x1	x2	y
590	32.64333333	13.2125
19	32.58166667	17.19166667
228	32.04666667	16.23541667
9	31.93833333	18.175
20	31.465	18.21458333
14	32.71166667	17.3125
350	32.71166667	14.68333333
57	32.12333333	17.03125
276	32	16.68958333
250	32.385	15.15
8	32.06333333	17.31458333
260	32.24	15.60208333
6	31.87666667	18.28333333
134	31.84333333	17.2375
154	31.73	17.26875
20	32.40833333	17.00625
3	31.57833333	18.59166667

【Excel】

エクセルの分析ツールの回帰分析を使います。

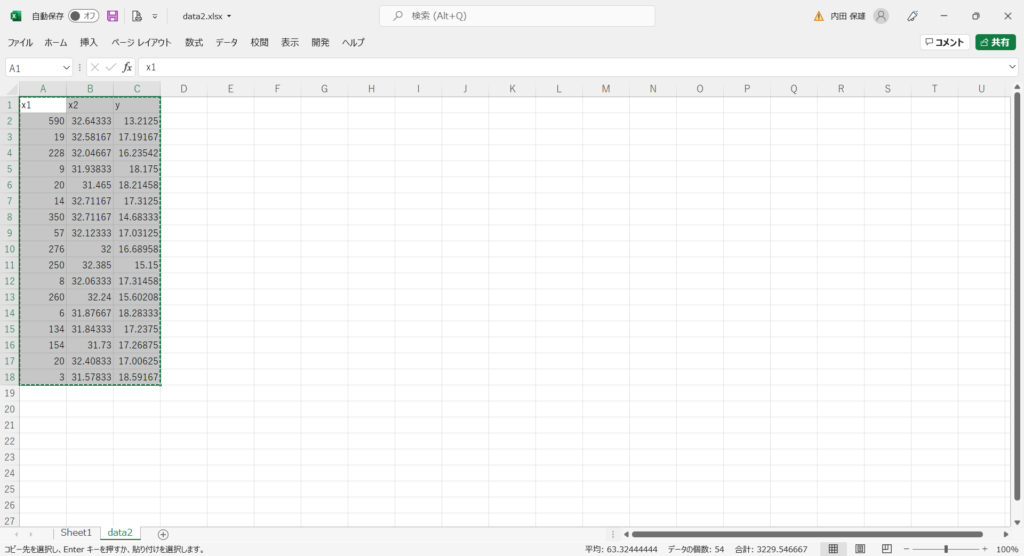
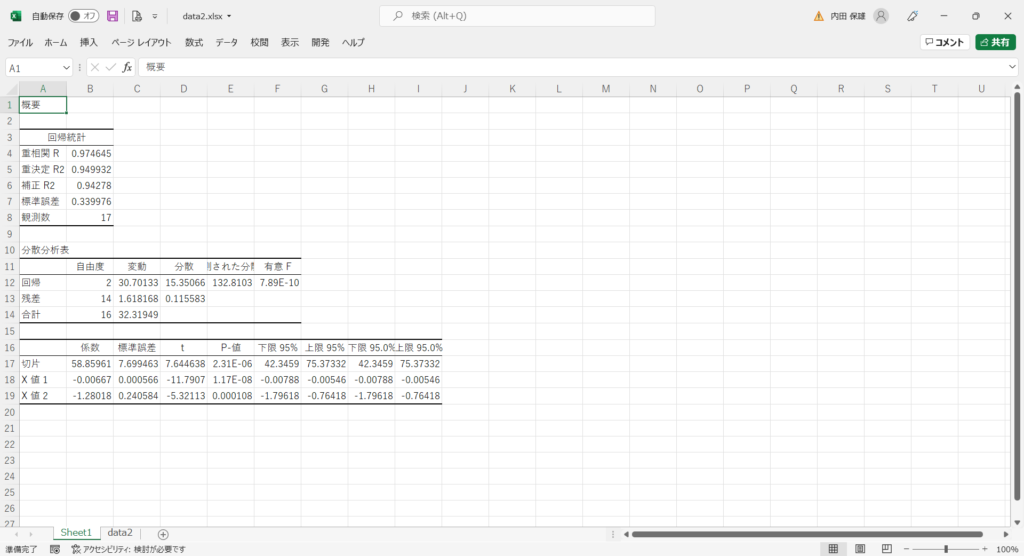
上の結果より、回帰式は「y = -0.00667×1 -1.28018×2 + 58.85961」となります。

なお、詳細は割愛しますが、予測精度が単回帰分析の場合より向上しています。

【Python】

　Pythonで同様の処理をおこない、回帰変数と切片を表示します。Excelの結果と一致していることが確認できます。

〔実行例〕

[[-0.00666881 -1.28017902]]
[58.85960881]

〔プログラム〕

import pandas as pd
import matplotlib.pyplot as plt
from sklearn import linear_model

df = pd.read_csv('data2.csv')

x = df[['x1','x2']]
y = df[['y']]

model = linear_model.LinearRegression()
model.fit(x, y)
print(model.coef_)
print(model.intercept_)
#print(model.score(x, y))
# 0.9499321410878981

---

Copyright (C) 2022 Easy Programming